Zadanie nr 9064751
Punkty 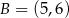 i
i 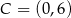 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 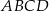 , którego podstawy
, którego podstawy 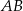 i
i 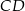 są prostopadłe do prostej
są prostopadłe do prostej 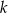 o równaniu
o równaniu 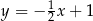 . Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt
. Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt 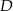 należy do prostej
należy do prostej 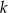 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
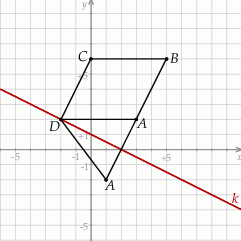
Wierzchołek 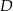 to punkt wspólny prostej
to punkt wspólny prostej 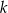 i prostej prostopadłej do
i prostej prostopadłej do 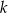 i przechodzącej przez punkt
i przechodzącej przez punkt 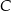 . Napiszmy równanie tej prostej. Jest ona prostopadła do
. Napiszmy równanie tej prostej. Jest ona prostopadła do 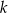 , więc ma równanie postaci
, więc ma równanie postaci 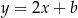 . Współczynnik
. Współczynnik 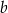 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 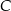 .
.
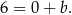
Zatem prosta 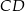 ma równanie
ma równanie 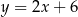 . Szukamy jej punktu wspólnego z prostą
. Szukamy jej punktu wspólnego z prostą 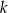 .
.
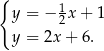
Odejmujemy od drugiego równania pierwsze i mamy
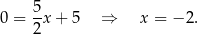
Stąd 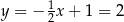 i
i 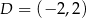 .
.
Napiszemy teraz równanie prostej 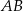 . Jako prostopadła do
. Jako prostopadła do 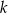 ma ona równanie postaci
ma ona równanie postaci 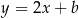 . Współczynnik
. Współczynnik 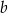 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 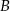 .
.
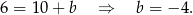
Zatem prosta 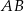 ma równanie:
ma równanie: 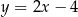 , co oznacza, że punkt
, co oznacza, że punkt 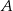 ma współrzędne postaci
ma współrzędne postaci 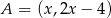 . Pozostało teraz wykorzystać informację o tym, że trapez jest równoramienny.
. Pozostało teraz wykorzystać informację o tym, że trapez jest równoramienny.
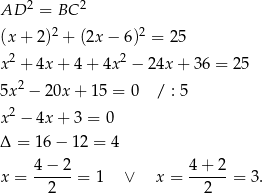
Mamy wtedy odpowiednio 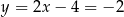 i
i 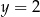 . Stąd
. Stąd 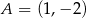 lub
lub 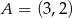 .
.
Odpowiedź: 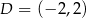 ,
, 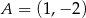 lub
lub