Zadanie nr 9510956
Przekątne deltoidu 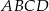 przecinają się w punkcie
przecinają się w punkcie 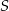 , który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie
, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie 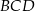 jeżeli okręgi opisane na trójkątach
jeżeli okręgi opisane na trójkątach 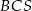 i
i 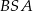 mają odpowiednio równania
mają odpowiednio równania 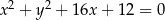 i
i 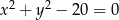 .
.
Rozwiązanie
Rozpoczynamy od schematycznego rysunku.
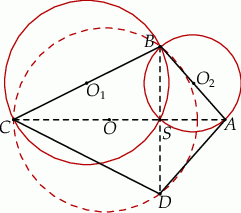
Z podanych równań okręgów łatwo wyznaczyć współrzędne ich punktów przecięcia.
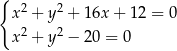
Odejmujemy od pierwszego równania drugie i mamy
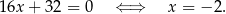
Podstawiamy tę wartość do drugiego równania układu.
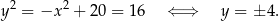
W takim razie punkty wspólne dwóch danych okręgów to 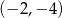 i
i 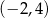 . Wiemy, że punkt
. Wiemy, że punkt 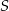 znajduje się w III ćwiartce układu, więc musimy mieć
znajduje się w III ćwiartce układu, więc musimy mieć 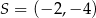 oraz
oraz 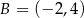 .
.
Ponieważ przekątne deltoidu są prostopadłe, a prosta 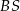 jest pionowa, przekątna
jest pionowa, przekątna 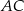 jest poziomą prostą przechodzącą przez punkt
jest poziomą prostą przechodzącą przez punkt 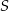 , czyli prostą
, czyli prostą 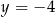 . Możemy więc teraz łatwo wyznaczyć współrzędne punktu
. Możemy więc teraz łatwo wyznaczyć współrzędne punktu 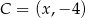 . Podstawiamy współrzędne tego punktu do równania okręgu opisanego na trójkącie
. Podstawiamy współrzędne tego punktu do równania okręgu opisanego na trójkącie 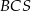 .
.
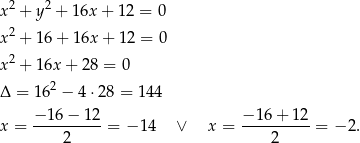
Drugie rozwiązanie prowadzi do punktu 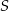 , więc wybieramy pierwsze rozwiązanie, czyli
, więc wybieramy pierwsze rozwiązanie, czyli 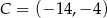 .
.
Trójkąt 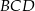 jest trójkątem równoramiennym, więc jego środek okręgu opisanego leży na prostej
jest trójkątem równoramiennym, więc jego środek okręgu opisanego leży na prostej 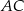 , czyli ma współrzędne postaci
, czyli ma współrzędne postaci 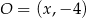 . Punkt ten musi znajdować się w tej samej odległości od wierzchołków trójkąta
. Punkt ten musi znajdować się w tej samej odległości od wierzchołków trójkąta 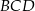 , co pozwala wyznaczyć pierwszą współrzędną punktu
, co pozwala wyznaczyć pierwszą współrzędną punktu 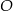 .
.
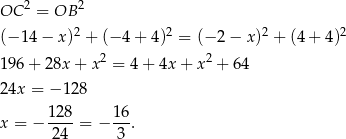
Zatem 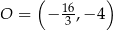 . Pozostało teraz obliczyć odległość punktów
. Pozostało teraz obliczyć odległość punktów 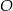 i
i 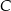 .
.
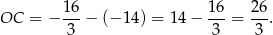
Okrąg opisany na trójkącie 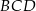 ma więc równanie
ma więc równanie
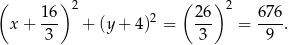
Na koniec odrobinę dokładniejszy rysunek całej sytuacji.
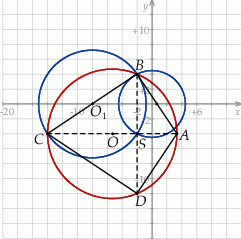
Odpowiedź: