/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 9520334

Dodaj do ulubionych
Dodaj do rozwiązanych

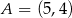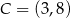W układzie współrzędnych na płaszczyźnie punkty A = (5,4) i C = (3,8) są przeciwległymi wierzchołkami kwadratu 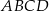ABCD . Wyznacz równanie prostej BD .

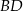Rozwiązanie

Rozpoczynamy od szkicowego rysunku

PIC

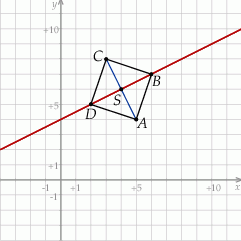
Z obrazka widzimy, że musimy napisać równanie prostej prostopadłej do prostej 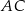AC i przechodzącej przez środek odcinka 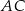AC , czyli przez punkt

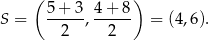
( ) 5-+-3-4-+-8- S = 2 , 2 = (4,6).

Zrobimy to na trzy sposoby.

Sposób I

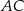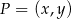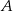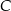Szukana prosta jest symetralną odcinka AC , czyli zbiorem punktów P = (x,y) , które są w tej samej odległości od punktów A i C . Otrzymujemy stąd równanie

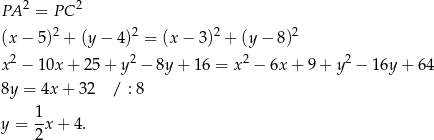
PA 2 = P C2 2 2 2 2 (x − 5) + (y − 4) = (x − 3) + (y − 8) x2 − 10x + 2 5+ y2 − 8y+ 16 = x2 − 6x + 9 + y2 − 16y + 64 8y = 4x + 32 / : 8 1 y = -x + 4. 2

Sposób II

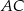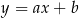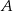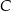Zacznijmy od napisania równania prostej AC . Szukamy prostej postaci y = ax+ b . Podstawiając współrzędne punktów A i C otrzymujemy układ równań.

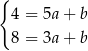
{ 4 = 5a+ b 8 = 3a+ b

Odejmując od pierwszego równania drugie (żeby skrócić 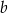b ) mamy

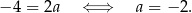
− 4 = 2a ⇐ ⇒ a = − 2.

I dalej możemy nie liczyć, bo potrzebny nam jest tylko współczynnik kierunkowy. Zatem prosta 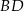BD , jako prostopadła do 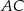AC musi mieć współczynnik kierunkowy 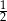12 , czyli jest postaci 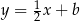y = 12x + b dla pewnego 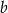b . Współczynnik 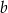b wyliczamy podstawiając współrzędne punktu S = (4,6) .

1 6 = 2-⋅4 + b ⇐ ⇒ b = 6− 2 = 4.

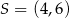Zatem szukana prosta ma równanie 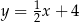y = 1x + 4 2 .

Sposób III

Tym razem skorzystamy ze wzoru

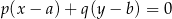
p(x − a )+ q(y − b ) = 0

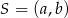na równanie prostej prostopadłej do wektora →v = [p ,q] i przechodzącej przez punkt S = (a ,b ) . W naszej sytuacji mamy

→ → v = AC = [3 − 5,8 − 4] = [− 2,4],

oraz

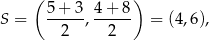
( 5 + 3 4 + 8 ) S = -----,------ = (4,6), 2 2

czyli równanie prostej 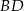BD ma postać:

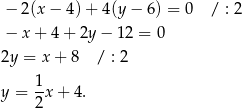
− 2(x − 4) + 4(y − 6 ) = 0 / : 2 − x + 4 + 2y − 12 = 0 2y = x + 8 / : 2 1- y = 2x + 4 .

 
Odpowiedź: y = 1x + 4 2

Wersja PDF