/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Romb

Zadanie nr 2393166

Punkty przecięcia paraboli 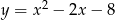2 y = x − 2x − 8 z prostą 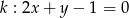k : 2x + y − 1 = 0 są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.

Wersja PDF

Rozwiązanie

Wyznaczmy najpierw współrzędne punktów wspólnych podanych: paraboli i prostej.

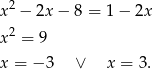
2 x − 2x− 8 = 1 − 2x x2 = 9 x = − 3 ∨ x = 3.

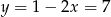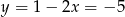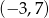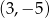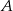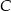Mamy wtedy odpowiednio y = 1 − 2x = 7 i y = 1 − 2x = − 5 . Zatem dwa wierzchołki rombu mają współrzędne (− 3,7) i (3,− 5) . Powiedzmy, że są to wierzchołki A i C . Wykonujemy teraz szkicowy rysunek.

PIC

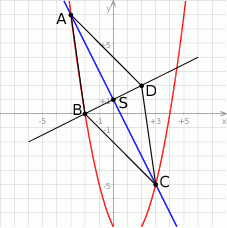
Obliczmy długość przekątnej 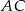AC .

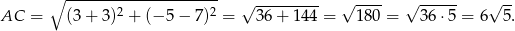
∘ --------------------- √ --------- √ ---- √ ------ √ -- AC = (3+ 3)2 + (−5 − 7)2 = 36+ 144 = 1 80 = 36 ⋅5 = 6 5 .

Z podanego pola i ze wzoru z przekątnymi na pole możemy więc wyliczyć długość drugiej przekątnej.

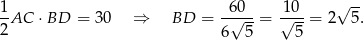
1-AC ⋅ BD = 30 ⇒ BD = -6√0--= √10-= 2√ 5. 2 6 5 5

Wyznaczmy jeszcze punkt przecięcia przekątnych

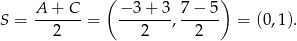
( ) A--+-C- −-3+--3 7-−-5- S = 2 = 2 , 2 = (0,1).

Mamy więc

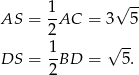
1- √ -- AS = 2AC = 3 5 1 √ -- DS = --BD = 5. 2

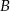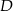Współrzędne punktów B i D obliczymy na dwa sposoby.

Sposób I

Zauważmy, że

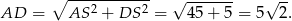
∘ ------------ √ ------- √ -- AD = AS 2 + DS 2 = 45+ 5 = 5 2.

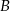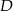Zatem punkty B i D to punkty wspólne okręgu o środku 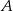A i promieniu 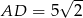√ -- AD = 5 2 oraz okręgu o środku 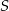S i promieniu 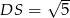√ -- DS = 5 . Mamy więc układ równań

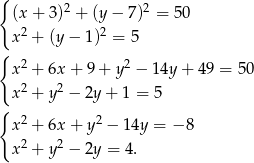
{ (x + 3)2 + (y − 7)2 = 5 0 x 2 + (y − 1)2 = 5 { 2 2 x + 6x + 9 + y − 1 4y+ 49 = 50 x 2 + y2 − 2y + 1 = 5 { x 2 + 6x + y 2 − 1 4y = − 8 2 2 x + y − 2y = 4.

Odejmujemy teraz od pierwszego równania drugie (żeby zredukować kwadraty) i mamy

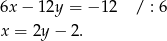
6x− 12y = − 12 / : 6 x = 2y − 2.

Podstawiamy teraz 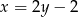x = 2y − 2 do drugiego równania okręgu,

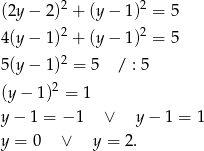
2 2 (2y − 2) + (y − 1) = 5 4(y − 1)2 + (y − 1)2 = 5 5(y − 1)2 = 5 / : 5 2 (y − 1) = 1 y − 1 = − 1 ∨ y − 1 = 1 y = 0 ∨ y = 2.

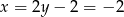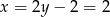Mamy wtedy x = 2y − 2 = − 2 i x = 2y − 2 = 2 odpowiednio. Zatem 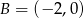B = (− 2,0) i D = (2,2) .

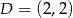Sposób II

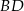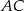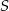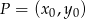
Tym razem napiszmy równanie przekątnej BD , czyli prostej prostopadłej do AC i przechodzącej przez S . Napiszemy równanie tej prostej korzystając ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt P = (x0,y0)

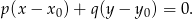
p(x − x0) + q(y − y0) = 0 .

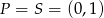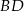W naszej sytuacji mamy P = S = (0,1) i −→ →v = AS = [0 + 3,1 − 7] = [3,− 6] . Prosta BD ma więc równanie

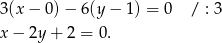
3(x − 0)− 6(y − 1) = 0 / : 3 x− 2y + 2 = 0.

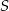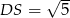Szukamy teraz na tej prostej punktów, które są odległe od S o √ -- DS = 5 , czyli punktów wspólnych z okręgiem

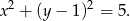
x2 + (y − 1)2 = 5.

Podstawiamy do tego równania okręgu 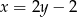x = 2y − 2 .

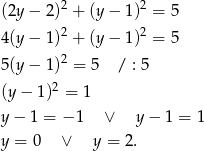
(2y − 2)2 + (y − 1)2 = 5 2 2 4(y − 1) + (y − 1) = 5 2 5(y − 1) = 5 / : 5 (y − 1)2 = 1 y − 1 = − 1 ∨ y − 1 = 1 y = 0 ∨ y = 2.

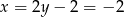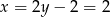Mamy wtedy x = 2y − 2 = − 2 i x = 2y − 2 = 2 odpowiednio. Zatem 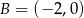B = (− 2,0) i D = (2,2) .  
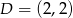Odpowiedź: (− 3,7),(− 2,0),(3,− 5),(2,2 )

Wersja PDF