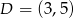Zadanie nr 5262946
W rombie 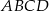 , którego pole jest równe 10 dane są przeciwległe wierzchołki
, którego pole jest równe 10 dane są przeciwległe wierzchołki 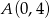 i
i 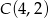 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Rozwiązanie
Jest kilka sposobów rozwiązania tego zadania, my pokażemy jeden z nich. Najważniejsza w tym zadaniu jest dokładna analiza schematycznego rysunku.
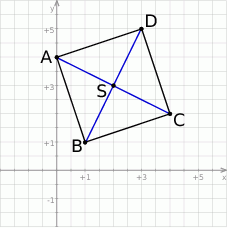
Pozostałe wierzchołki byłoby łatwo wyliczyć gdybyśmy znali długość boku rombu. Tę długość możemy wyliczyć z trójkąta prostokątnego 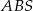 pod warunkiem, że znamy długości przekątnych. Z przekątną
pod warunkiem, że znamy długości przekątnych. Z przekątną 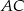 nie ma problemu
nie ma problemu
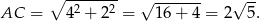
Jeżeli chodzi o drugą przekątną, to skorzystamy ze wzoru na pole rombu
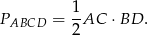
Stąd
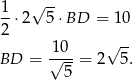
Zamiast korzystać ze wzoru na pole rombu, mogliśmy zauważyć, że pole trójkąta 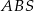 jest równe
jest równe 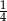 pola całego rombu i skorzystać ze wzoru na pole trójkąta prostokątnego.
pola całego rombu i skorzystać ze wzoru na pole trójkąta prostokątnego.
Liczymy teraz długość boku rombu
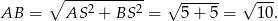
Szukamy teraz punktów, które są odległe od  i
i  o
o  (lub jak kto woli przecinamy dwa okręgi o środkach w tych punktach i promieniu
(lub jak kto woli przecinamy dwa okręgi o środkach w tych punktach i promieniu 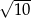 ). Aby nie mieć pierwiastków, od razu piszemy kwadraty odległości
). Aby nie mieć pierwiastków, od razu piszemy kwadraty odległości
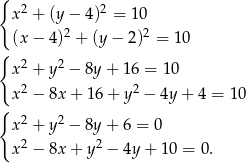
Odejmując te równania stronami (żeby skrócić kwadraty) mamy

Podstawiamy to do pierwszego równania układu i mamy
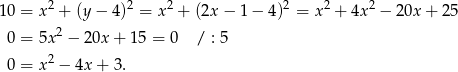
Dalej, 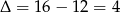 ,
, 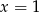 lub
lub 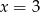 . Mamy wtedy
. Mamy wtedy 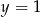 i
i 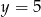 odpowiednio.
odpowiednio.
Odpowiedź: 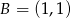 ,
,