Zadanie nr 5277998
Oblicz pole i obwód rombu 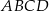 wiedząc, że przekątna
wiedząc, że przekątna 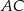 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 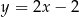 oraz
oraz 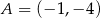 i
i 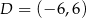 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
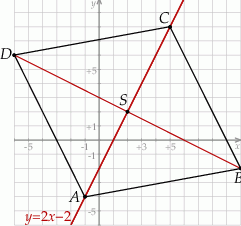
Ponieważ znamy dwa kolejne wierzchołki rombu, nie ma problemu z obliczeniem jego obwodu.
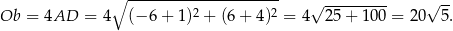
Pozostało teraz obliczyć pole – zrobimy to korzystając ze wzoru na pole z przekątnymi. Zauważmy, że dość łatwo możemy napisać równanie prostej zawierającej przekątną 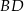 rombu – jest to prosta prostopadła do
rombu – jest to prosta prostopadła do 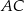 i przechodząca przez
i przechodząca przez 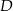 . Szukamy więc prostej w postaci
. Szukamy więc prostej w postaci 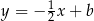 , współczynnik
, współczynnik 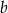 obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 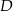 .
.
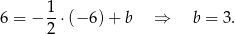
Zatem prosta 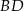 ma równanie
ma równanie 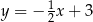 . Możemy teraz obliczyć współrzędne środka rombu
. Możemy teraz obliczyć współrzędne środka rombu 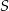 – jest to punkt wspólny przekątnych
– jest to punkt wspólny przekątnych 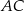 i
i 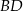 .
.
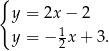
Odejmujemy od pierwszego równania drugie i mamy
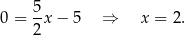
Stąd 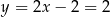 i
i 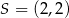 . Obliczamy teraz długości przekątnych rombu
. Obliczamy teraz długości przekątnych rombu
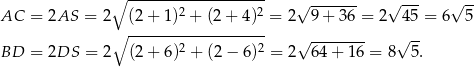
Pole rombu jest więc równe
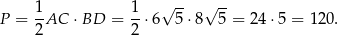
Odpowiedź: Obwód: 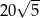 , pole: 120.
, pole: 120.

