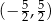Zadanie nr 5527849
Na okręgu o równaniu 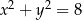 opisano romb o polu
opisano romb o polu 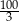 . Dłuższa przekątna rombu zawiera się w prostej o równaniu
. Dłuższa przekątna rombu zawiera się w prostej o równaniu 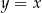 . Oblicz współrzędne wierzchołków tego rombu.
. Oblicz współrzędne wierzchołków tego rombu.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
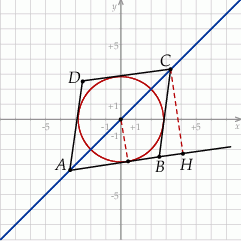
Ponieważ przekątne rombu są dwusiecznymi jego kątów wewnętrznych to środek okręgu wpisanego w romb pokrywa się z punktem przecięcia wysokości. Ponadto promień okręgu wpisanego to dokładnie połowa wysokości rombu. Możemy więc zapomnieć o okręgu wpisanym i pamiętać, że mamy środek 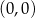 i wysokość rombu
i wysokość rombu 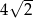 .
.
Ponieważ mamy podane pole rombu, możemy obliczyć długość jego boku
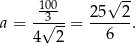
Mając długość boku i wysokość rombu możemy obliczyć długości przekątnych. Z trójkąta prostokątnego 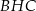 mamy
mamy
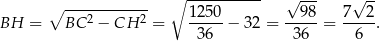
Zatem 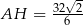 i możemy obliczyć długość przekątnej
i możemy obliczyć długość przekątnej 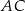
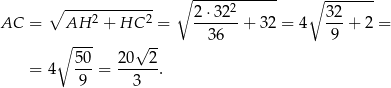
Szukamy teraz na prostej 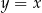 punktów w odległości
punktów w odległości 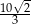 od punktu
od punktu 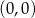
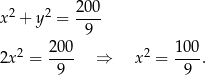
Stąd 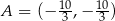 i
i 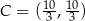 .
.
Punkty  i
i 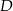 leżą na prostej prostopadłej do
leżą na prostej prostopadłej do 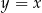 i przechodzącej przez
i przechodzącej przez  , czyli na prostej
, czyli na prostej 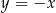 . Ponadto ich odległość od punktu
. Ponadto ich odległość od punktu 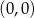 (ze wzoru na pole
(ze wzoru na pole 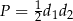 ), to:
), to:
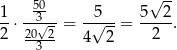
Szukamy punktów 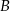 i
i 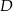 .
.
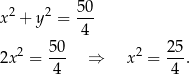
Stąd 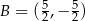 ,
, 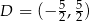 .
.
Odpowiedź: 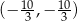 ,
, 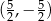 ,
, 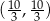 ,
,