Zadanie nr 6287844
W rombie 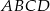 dane są
dane są 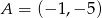 i punkt przecięcia przekątnych
i punkt przecięcia przekątnych 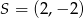 . Wierzchołek
. Wierzchołek 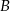 leży na prostej
leży na prostej 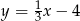 . Oblicz współrzędne pozostałych wierzchołków rombu.
. Oblicz współrzędne pozostałych wierzchołków rombu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
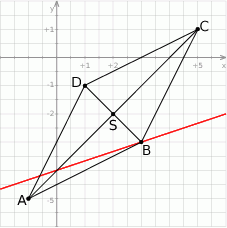
Ponieważ przekątne rombu dzielą się na połowy, punkt 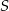 jest środkiem odcinków
jest środkiem odcinków 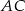 i
i 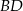 . To pozwala łatwo wyznaczyć współrzędne punktu
. To pozwala łatwo wyznaczyć współrzędne punktu 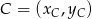 .
.
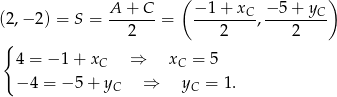
Zatem 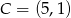 .
.
Możemy teraz napisać równanie przekątnej 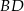 rombu – jest to prosta prostopadła do
rombu – jest to prosta prostopadła do 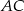 i przechodząca przez
i przechodząca przez 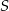 . Równanie prostej
. Równanie prostej 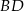 napiszemy na kilka sposobów.
napiszemy na kilka sposobów.
Sposób I
Jeżeli punkt 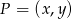 leży na prostej
leży na prostej 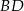 to
to
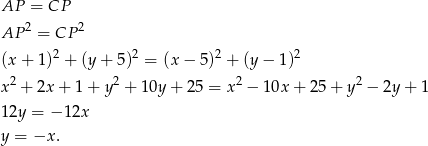
Szukamy teraz punktu wspólnego 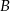 prostych
prostych 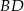 i danej prostej
i danej prostej 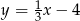 .
.
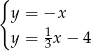
Mamy zatem
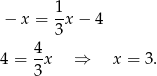
Stąd 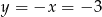 i
i 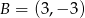 . Pozostało wyznaczyć współrzędne punktu
. Pozostało wyznaczyć współrzędne punktu 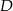 .
.
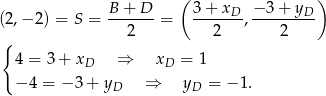
Zatem 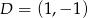 .
.
Sposób II
Równanie prostej 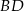 możemy napisać jako równanie prostej prostopadłej do
możemy napisać jako równanie prostej prostopadłej do 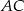 i przechodzącej przez
i przechodzącej przez 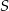 . Najpierw wyznaczmy równanie prostej
. Najpierw wyznaczmy równanie prostej 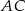 . Szukamy prostej w postaci
. Szukamy prostej w postaci 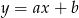 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 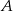 i
i 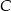 mamy
mamy
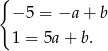
Odejmujemy od drugiego równania pierwsze i mamy 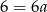 , czyli
, czyli 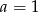 . Współczynnika
. Współczynnika 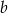 możemy nie obliczać, bo nie jest nam potrzebny. Prosta
możemy nie obliczać, bo nie jest nam potrzebny. Prosta 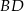 jako prostopadła do
jako prostopadła do 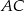 ma równanie postaci
ma równanie postaci 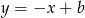 . Współczynnik
. Współczynnik 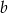 wyznaczmy podstawiając współrzędne punktu
wyznaczmy podstawiając współrzędne punktu 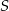 .
.
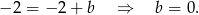
Zatem prosta 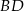 ma równanie
ma równanie 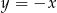 . Współrzędne punktów
. Współrzędne punktów 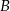 i
i 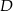 wyznaczamy tak samo jak w poprzednim sposobie.
wyznaczamy tak samo jak w poprzednim sposobie.
Sposób III
Równanie prostej 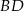 można łatwo napisać korzystając ze wzoru na równanie prostej prostopadłej do wektora
można łatwo napisać korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/6287844/HzadR46x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 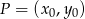
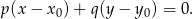
W naszej sytuacji
![→v = −A→C = [5 + 1,1 + 5] = [6,6]](https://img.zadania.info/zad/6287844/HzadR49x.gif)
i 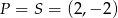 . Prosta
. Prosta 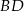 ma więc równanie
ma więc równanie
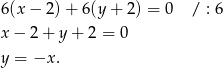
Współrzędne punktów 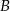 i
i 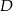 wyznaczamy tak samo jak w I sposobie.
wyznaczamy tak samo jak w I sposobie.
Odpowiedź: