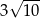/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Romb

Zadanie nr 6761383

Punkt 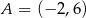A = (− 2,6) jest wierzchołkiem rombu 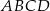ABCD o polu 90. Przekątna 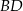BD zawiera się w prostej 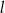l o równaniu 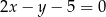2x − y − 5 = 0 . Wyznacz długość boku tego rombu.

Wersja PDF

Rozwiązanie

Zaczynamy oczywiście od schematycznego rysunku.

PIC

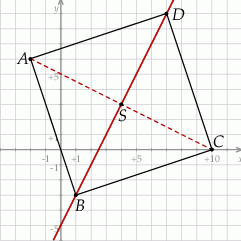
Sposób I

Jeżeli 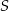S jest środkiem rombu, to łatwo obliczyć długość odcinka 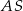AS – jest to odległość punktu 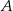A od danej prostej 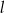l . Mamy zatem

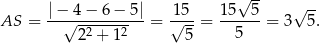
√ -- |-−-4-−-6-−-5| -15- 15---5 √ -- AS = √ -2----2 = √ 5-= 5 = 3 5. 2 + 1

To z kolei pozwala łatwo obliczyć długość odcinka 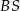BS – korzystamy z podanego pola rombu.

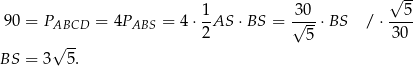
√ -- 90 = PABCD = 4PABS = 4 ⋅ 1-AS ⋅BS = 3√0--⋅BS / ⋅--5- 2 5 30 √ -- BS = 3 5.

Pozostało obliczyć długość boku rombu – korzystamy tego, że przekątne rombu są prostopadłe (oczywiście zamiast tego możemy zauważyć, że dany romb to kwadrat).

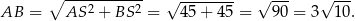
∘ ----------- √ -------- √ --- √ --- AB = AS 2 + BS 2 = 45 + 4 5 = 90 = 3 10.

Sposób II

Jeżeli jesteśmy mniej sprytni, to możemy powyznaczać współrzędne wierzchołków rombu. Na przykład prosta 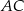AC ma równanie postaci 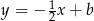y = − 1x+ b 2 (bo jest prostopadła do 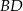BD ) i przechodzi przez 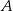A , więc

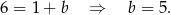
6 = 1+ b ⇒ b = 5.

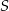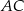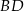Punkt S jest punktem wspólnym prostych AC i BD , czyli jego współrzędne są rozwiązaniami układu równań

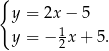
{ y = 2x − 5 y = − 12 x+ 5.

Odejmujemy równania stronami i mamy

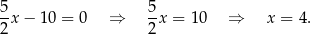
5- 5- 2x − 10 = 0 ⇒ 2x = 10 ⇒ x = 4.

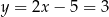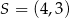Stąd y = 2x − 5 = 3 i S = (4 ,3 ) . W takim razie

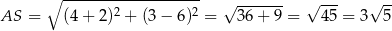
∘ ------------------- √ ------- √ --- √ -- AS = (4+ 2)2 + (3 − 6 )2 = 36+ 9 = 45 = 3 5

i

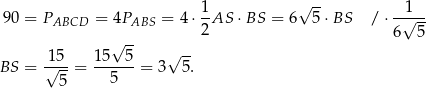
√ -- 90 = P = 4P = 4 ⋅ 1-AS ⋅BS = 6 5⋅BS /⋅ -1√--- ABCD ABS 2 6 5 √ -- √ -- BS = 1√5--= 15--5-= 3 5. 5 5

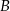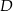Wierzchołki B i D mają współrzędne postaci 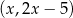(x ,2x− 5) oraz

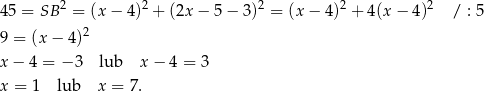
45 = SB 2 = (x − 4)2 + (2x − 5 − 3)2 = (x − 4 )2 + 4(x − 4 )2 / : 5 9 = (x − 4)2 x− 4 = − 3 lub x − 4 = 3 x = 1 lub x = 7.

Wybieramy którekolwiek z rozwiąząń i mamy np. 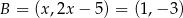B = (x ,2x− 5) = (1,− 3) . Stąd

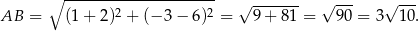
∘ --------------------- √ ------- √ --- √ --- AB = (1 + 2)2 + (− 3− 6)2 = 9+ 81 = 90 = 3 10.

 
Odpowiedź: √ --- 3 10

Wersja PDF