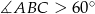Zadanie nr 9275549
Dany jest romb o środku symetrii 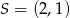 . Bok
. Bok 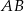 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu 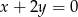 . Wektor
. Wektor 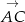 ma współrzędne
ma współrzędne ![[12 ,6 ]](https://img.zadania.info/zad/9275549/HzadT4x.gif) .
.
- Wyznacz współrzędne wszystkich wierzchołków rombu.
- Sprawdź czy miara kąta
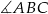 jest większa niż
jest większa niż 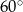 .
.
Rozwiązanie
- Zacznijmy od rysunku.
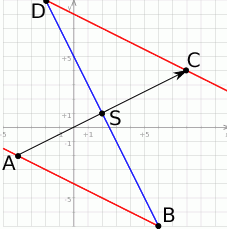
Jeżeli narysujemy dany wektor
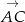 tak aby jego środkiem był punkt
tak aby jego środkiem był punkt 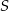 , to końcami tego wektora będą punkty
, to końcami tego wektora będą punkty 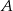 i
i 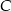 . Wyznaczmy te punkty.
. Wyznaczmy te punkty. ![→ → → → AS = 1-AC SC = 1AC 2 2 [2− x,1− y] = [6,3] [x − 2 ,y− 1] = [6,3 ] A = (x,y) = (− 4,− 2) C = (x ,y) = (8,4).](https://img.zadania.info/zad/9275549/HzadR5x.gif)
Mając punkt
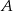 możemy napisać równanie prostej
możemy napisać równanie prostej 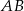 . Jest ona postaci
. Jest ona postaci 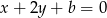 i przechodzi przez
i przechodzi przez 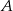 . Zatem
. Zatem 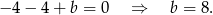
Podobnie wyznaczamy równanie prostej
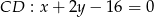 .
. Dalszy plan jest następujący, napiszemy równanie drugiej przekątnej, czyli prostej prostopadłej do wektora
 i przechodzącej przez
i przechodzącej przez  , a na koniec znajdziemy jej punkty wspólne z prostymi
, a na koniec znajdziemy jej punkty wspólne z prostymi 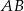 i
i 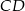 . Aby napisać równanie prostej
. Aby napisać równanie prostej 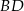 , korzystamy ze wzoru na równanie prostej prostopadłej do wektora
, korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/9275549/HzadR17x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 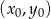
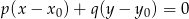
W naszej sytuacji
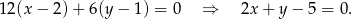
Przecinamy ją z prostą
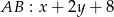 (od razu podstawiamy za
(od razu podstawiamy za 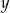 )
) 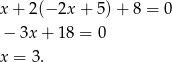
Zatem
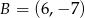 . Podobnie, przecinamy ją z prostą
. Podobnie, przecinamy ją z prostą 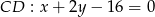 .
. 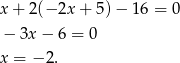
Zatem
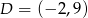 .
.
Odpowiedź: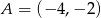 ,
, 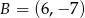 ,
, 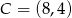 ,
, 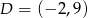
- Obliczymy cosinus kąta
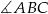 . Mamy
. Mamy ![→ BA = [− 10,5]](https://img.zadania.info/zad/9275549/HzadR33x.gif) ,
, ![→ BC = [2,11]](https://img.zadania.info/zad/9275549/HzadR34x.gif) . Stąd
. Stąd 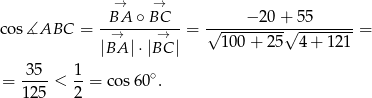
Ponieważ
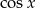 jest malejący w przedziale
jest malejący w przedziale 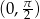 , nierówność ta oznacza, że
, nierówność ta oznacza, że 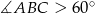 .
.
Odpowiedź: