/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 4139267

Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.

Wersja PDF

Rozwiązanie

Oznaczmy dany ciąg przez 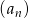(an) . Z podanych informacji wynika, że jest to ciąg arytmetyczny o pierwszym wyrazie 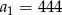a1 = 444 i różnicy 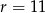r = 11 . Mamy więc

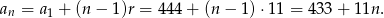
an = a1 + (n − 1)r = 44 4+ (n − 1)⋅11 = 433 + 11n .

Obliczmy teraz, ile wyrazów ma ten ciąg.

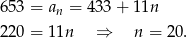
653 = an = 433 + 11n 220 = 11n ⇒ n = 20.

Pozostało obliczyć sumę wszystkich wyrazów tego ciągu.

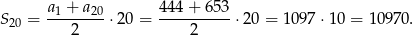
a1 + a20 4 44+ 653 S20 = -------- ⋅20 = ---------- ⋅20 = 1 097⋅ 10 = 1097 0. 2 2

 
Odpowiedź: 10970

Wersja PDF