/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 5331944

Ciąg 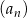(an) jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym 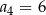a 4 = 6 . Ciąg 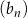(bn ) dla dowolnego 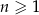n ≥ 1 spełnia warunek 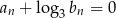an + log3 bn = 0 . Oblicz granicę

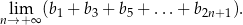
lim (b1 + b3 + b5 + ... + b2n+1). n→ +∞
Wersja PDF

Rozwiązanie

Wyznaczmy najpierw wzór ciągu 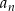an .

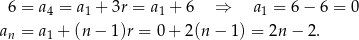
6 = a = a + 3r = a + 6 ⇒ a = 6 − 6 = 0 4 1 1 1 an = a1 + (n − 1)r = 0+ 2(n − 1) = 2n − 2.

Wyznaczmy teraz wzór ciągu 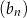(bn) .

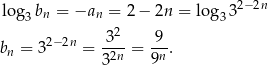
log3bn = −an = 2 − 2n = log 332− 2n 2 bn = 32−2n = 3---= -9-. 32n 9n

Widać teraz, że ciąg 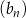(bn) jest ciągiem geometrycznym o pierwszym wyrazie równym 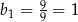b 1 = 99 = 1 i ilorazie 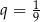q = 19 . Ciąg 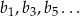b1,b 3,b 5... jest więc ciągiem geometrycznym o pierwszym wyrazie równym 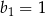b = 1 1 i ilorazie 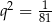q2 = 1- 81 . Suma wszystkich jego wyrazów jest więc równa

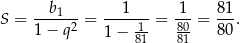
b1 1 1 8 1 S = -----2-= ----1--= 80-= ---. 1 − q 1− 81 81 8 0

 
Odpowiedź: 8810

Wersja PDF