/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 6807148

Dodaj do ulubionych
Dodaj do rozwiązanych

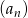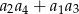Pierwszy wyraz ciągu arytmetycznego (an) wynosi 1. Dla jakiej wartości różnicy r wyrażenie a2a 4 + a1a3 ma wartość najmniejszą i ile ona wynosi?

Rozwiązanie

Ze wzoru 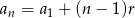an = a1 + (n − 1)r na n –ty wyraz ciągu arytmetycznego mamy

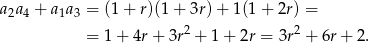
a2a4 + a1a3 = (1+ r)(1+ 3r)+ 1(1+ 2r) = = 1 + 4r+ 3r2 + 1+ 2r = 3r2 + 6r+ 2.

Otrzymaliśmy funkcję kwadratową, której wykresem jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie

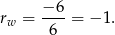
− 6 rw = ----= − 1. 6

Zatem dokładnie dla takiej różnicy interesujące nas wyrażenie przyjmuje wartość najmniejszą, która jest równa

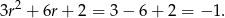
2 3r + 6r + 2 = 3− 6+ 2 = − 1.

 
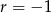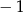Odpowiedź: r = − 1 , wartość najmniejsza: − 1 .

Wersja PDF