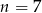/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 7594466

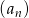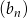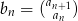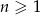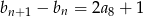Ciąg (an ) jest ciągiem arytmetycznym o różnicy 2, a ciąg (bn) zdefiniowany jest wzorem a bn = ( na+n1) , dla n ≥ 1 . Wyznacz wartość n , dla której bn+ 1 − bn = 2a8 + 1 .

Wersja PDF

Rozwiązanie

Liczymy

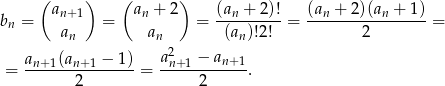
(a ) (a + 2) (a + 2)! (a + 2 )(a + 1) bn = n+1 = n = --n------ = ---n-------n----- = an an (an)!2! 2 a (a − 1) a 2 − an+1 = -n+1--n+-1----- = --n+1-------. 2 2

Mogliśmy też od razu skorzystać z własności

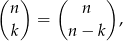
(n ) ( n ) = , k n − k

czyli

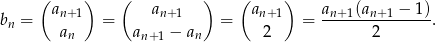
(a ) ( a ) (a ) a (a − 1) bn = n+ 1 = n+1 = n+1 = -n+-1--n+1-----. an an+ 1 − an 2 2

Musimy więc rozwiązać równanie

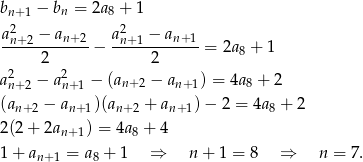
b − b = 2a + 1 n+ 1 n 8 a2n+ 2 − an+2 a2n+ 1 − an+1 ------2----- − ------2----- = 2a8 + 1 2 2 an+ 2 − an+ 1 − (an+2 − an+1) = 4a8 + 2 (an+ 2 − an+ 1)(an+2 + an+ 1)− 2 = 4a8 + 2 2(2 + 2an+ 1) = 4a8 + 4 1 + an+ 1 = a8 + 1 ⇒ n + 1 = 8 ⇒ n = 7.

 
Odpowiedź: n = 7

Wersja PDF