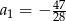/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 8452096

Ciąg 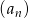(an ) jest ciągiem arytmetycznym, w którym 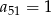a51 = 1 oraz wyrażanie 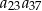a23a37 ma najmniejszą możliwą wartość. Wyznacz a1 .

Wersja PDF

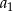Rozwiązanie

Z podanego wyrazu mamy

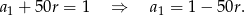
a1 + 50r = 1 ⇒ a1 = 1 − 50r.

Wyrażenie, o którym mowa w treści możemy zapisać w postaci

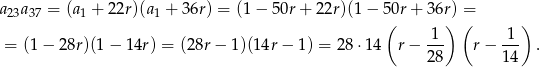
a23a37 = (a1 + 22r)(a1 + 36r) = (1 − 50r + 22r)(1 − 5(0r+ 3 6r)) =( ) -1- 1-- = (1 − 28r)(1 − 14r) = (28r− 1)(14r− 1) = 28 ⋅14 r − 2 8 r− 14 .

Otrzymaliśmy wzór funkcji kwadratowej (zmiennej r ), której wykresem jest parabola o ramionach skierowanych w górę. Zatem najmniejszą wartość wyrażenia otrzymamy dokładnie w wierzchołku, czyli dla

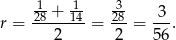
1-+ 1- -3 3 r = -28----14-= 28-= --. 2 2 56

Pozostało obliczyć odpowiadającą wartość 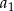a 1 .

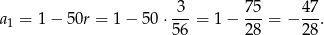
-3- 75- 47- a1 = 1 − 50r = 1 − 50 ⋅5 6 = 1 − 28 = − 28 .

 
Odpowiedź: a = − 47- 1 28

Wersja PDF