/Szkoła średnia/Ciągi/Arytmetyczny/Różne

Zadanie nr 9035984

Wartość pewnej frezarki maleje z roku na rok. Wartości tej frezarki w kolejnych latach tworzą ciąg arytmetyczny. Oblicz czas, w ciągu którego frezarka całkowicie straci wartość (zamortyzuje się), jeżeli wiadomo, że po 15 latach użytkowania jej wartość była 3 razy większa niż jej wartość po 25 latach.

Wersja PDF

Rozwiązanie

Sposób I

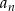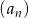Jeżeli oznaczymy przez an wartość frezarki w roku n , to ciąg (an) jest ciągiem arytmetycznym oraz wiemy, że

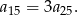
a15 = 3a25.

Korzystając ze wzoru na n -ty wyraz ciągu arytmetycznego mamy.

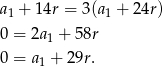
a1 + 14r = 3(a1 + 24r) 0 = 2a1 + 58r 0 = a1 + 29r.

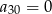Zatem a30 = 0 , co oznacza, że frezarka zamortyzuje się po 30 latach.

Sposób II

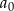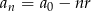Jeżeli oznaczymy przez a0 początkową wartość frezarki, to wartość frezarki po n latach wynosi an = a0 − nr , gdzie r jest kwotą, o którą zmniejsza się wartość urządzenia w ciągu roku. W takim razie podaną w treści zadania informację możemy zapisać jako równanie

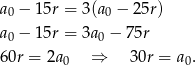
a − 1 5r = 3(a − 25r) 0 0 a0 − 1 5r = 3a0 − 75r 60r = 2a ⇒ 30r = a . 0 0

A co mamy obliczyć? Mamy obliczyć dla jakiego n będzie an = 0 .

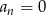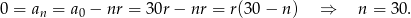
0 = an = a0 − nr = 30r− nr = r(30 − n ) ⇒ n = 30 .

 
Odpowiedź: Po 30 latach.

Wersja PDF