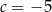Zadanie nr 3716670
Wykresem funkcji kwadratowej 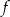 określonej wzorem
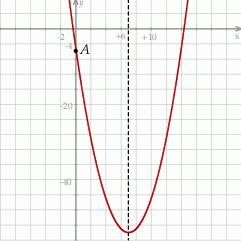
określonej wzorem 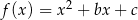 jest parabola, na której leży punkt
jest parabola, na której leży punkt 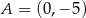 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 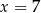 . Oblicz wartości współczynników
. Oblicz wartości współczynników 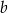 i
i  .
.
Rozwiązanie
Sposób I
Podana oś symetrii oznacza, że pierwsza współrzędna wierzchołka 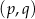 paraboli jest równa
paraboli jest równa 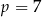 . Funkcja ma więc postać kanoniczną postaci
. Funkcja ma więc postać kanoniczną postaci
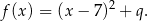
Współczynnik 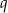 obliczamy korzystając z podanej informacji
obliczamy korzystając z podanej informacji 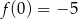 .
.
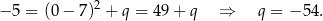
Zatem
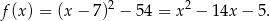
Sposób II
Wiemy, że
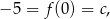
więc pozostało wyznaczyć 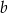 . Oś symetrii paraboli przechodzi przez jej wierzchołek, więc
. Oś symetrii paraboli przechodzi przez jej wierzchołek, więc
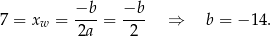
Na koniec wykres dla ciekawskich.
Odpowiedź: 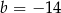 i
i