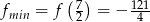Zadanie nr 5087961
Funkcja kwadratowa 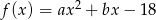 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 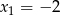 i
i 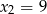 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Rozwiązanie
Sposób I
Na mocy wzorów Viète’a mamy
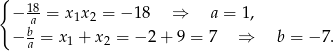
czyli
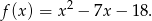
Ponadto, pierwsza współrzędna wierzchołka paraboli będącej wykresem funkcji 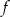 jest równa
jest równa
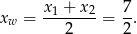
Najmniejsza wartość funkcji jest więc równa
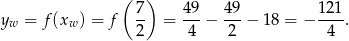
Sposób II
Podstawiamy podane wartości funkcji do danego wzoru funkcji 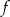 i otrzymujemy układ równań
i otrzymujemy układ równań
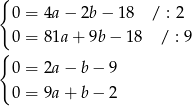
Dodajemy teraz równania stronami (żeby skrócić 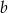 ) i mamy
) i mamy

Stąd 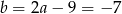 i
i
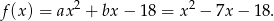
Pierwsza współrzędna wierzchołka paraboli będącej wykresem tej funkcji jest równa
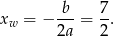
Najmniejsza wartość funkcji jest więc równa
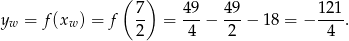
Odpowiedź: