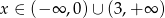/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem

Zadanie nr 6857709

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa 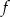f określona jest wzorem 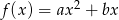2 f (x) = ax + bx . Wiadomo, że 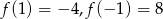f (1) = − 4,f(− 1) = 8 . Określ, dla jakich argumentów spełniona jest nierówność f(x) > 0 .

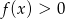Rozwiązanie

Podstawiamy podane wartości funkcji do danego wzoru funkcji 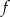f i otrzymujemy układ równań

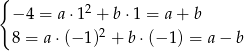
{ − 4 = a ⋅12 + b⋅ 1 = a+ b 8 = a ⋅(− 1)2 + b⋅ (− 1 ) = a− b

Dodajemy stronami do siebie równania i otrzymujemy

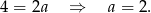
4 = 2a ⇒ a = 2.

Wyznaczamy 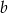b

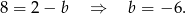
8 = 2− b ⇒ b = − 6.

Zatem funkcja 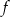f jest dana wzorem

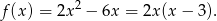
2 f(x ) = 2x − 6x = 2x(x − 3).

Widać, że pierwiastkami są liczby 0,3 oraz że wykres jest parabolą zwróconą gałęziami ku górze. Wykonujemy rysunek

PIC

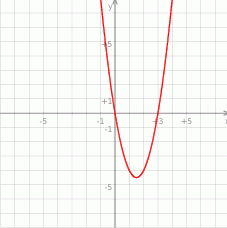
Łatwo odczytać, że nierówność 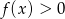f(x ) > 0 zachodzi dla

x ∈ (−∞ ,0 )∪ (3,+ ∞ ).

 
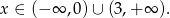
Odpowiedź: x ∈ (− ∞ ,0) ∪ (3,+ ∞ )

Wersja PDF