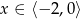/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem

Zadanie nr 9353293

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa 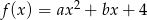2 f(x ) = ax + bx + 4 , osiąga wartości ujemne wtedy i tylko wtedy, gdy x ∈ (− ∞ ,− 3)∪ (1 ,+ ∞ ) .

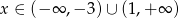  • Wyznacz wartości współczynników a i b .
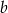  • Napisz postać kanoniczną funkcji f .
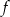  • Podaj wzór funkcji kwadratowej 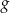g , której wykres otrzymamy przesuwając wykres funkcji 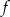f o wektor → u = [2,− 130] .
  • Wyznacz te argumenty x , dla których f (x) ≥ 4 .

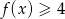Rozwiązanie

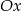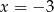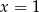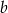  • Z podanej informacji wynika, że ramiona paraboli są skierowane w dół oraz przecina ona oś Ox w punktach x = − 3 i x = 1 . Współczynniki a i b możemy wyliczyć sprawdzając, kiedy te liczby są pierwiastkami danej funkcji. Prościej jednak jest skorzystać ze wzorów Viète’a.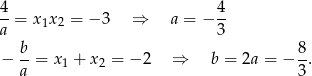
    4-= x x = − 3 ⇒ a = − 4- a 1 2 3 b 8 − a-= x1 + x2 = − 2 ⇒ b = 2a = − 3.

     
    Odpowiedź: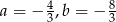 a = − 43,b = − 83

    PIC
  • Liczymy (zwijamy do pełnego kwadratu)
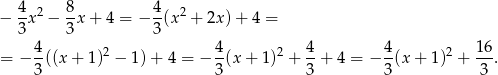
    4 8 4 − --x2 − -x + 4 = − -(x2 + 2x )+ 4 = 3 3 3 = − 4((x + 1)2 − 1)+ 4 = − 4-(x+ 1)2 + 4+ 4 = − 4-(x+ 1)2 + 16. 3 3 3 3 3

     
    Odpowiedź: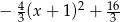 − 43(x + 1)2 + 136

  • Korzystamy ze wzoru na przesunięcie funkcji 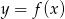y = f(x ) o wektor → v = [a,b] :
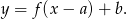
    y = f (x− a)+ b.

    W naszej sytuacji mamy

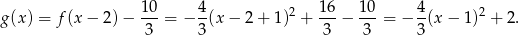
    g(x ) = f(x − 2) − 10-= − 4-(x − 2+ 1 )2 + 16-− 10-= − 4(x − 1 )2 + 2. 3 3 3 3 3

     
    Odpowiedź: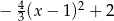 − 43(x − 1)2 + 2

  • Korzystamy od razu z postaci kanonicznej
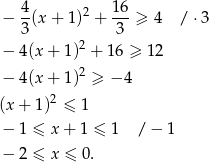
    − 4-(x+ 1)2 + 16-≥ 4 / ⋅3 3 3 − 4(x + 1)2 + 16 ≥ 1 2 − 4(x + 1)2 ≥ − 4 2 (x + 1) ≤ 1 − 1 ≤ x + 1 ≤ 1 / − 1 − 2 ≤ x ≤ 0.

     
    Odpowiedź: x ∈ ⟨− 2,0⟩

Wersja PDF