Zadanie nr 1611076
Wykaż, że dla wszystkich dodatnich liczb rzeczywistych 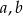 prawdziwa jest nierówność
prawdziwa jest nierówność 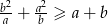 .
.
Rozwiązanie
Przekształcamy daną nierówność.
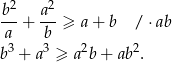
Dalsze przekształcenia wykonamy na 2 sposoby.
Sposób I
Przekształcamy nierówność korzystając ze wzoru na sumę sześcianów.
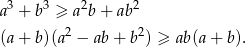
Jeżeli 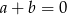 to nierówność jest oczywiście spełniona, więc załóżmy, że
to nierówność jest oczywiście spełniona, więc załóżmy, że 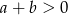 . Możemy wtedy podzielić stronami przez
. Możemy wtedy podzielić stronami przez 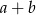 i mamy
i mamy
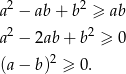
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.
Sposób II
Przekształcamy daną nierówność
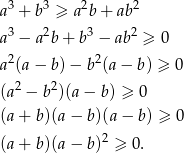
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.

