Zadanie nr 3151872
Na podstawie podanego wykresu funkcji 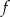
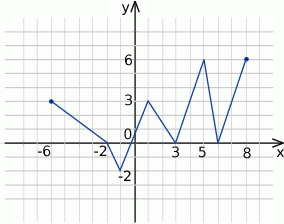
- wyznacz największą i najmniejszą wartość funkcji;
- podaj najdłuższy przedział na którym funkcja jest malejąca;
- zapisz w postaci sumy przedziałów zbiór rozwiązań nierówności
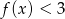 ;
; - oblicz w ilu punktach wykres funkcji
![g(x) = [f(x )]2](https://img.zadania.info/zad/3151872/HzadT3x.gif) przecina prostą
przecina prostą 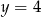 .
.
Rozwiązanie
- Odczytujemy z wykresu.
Odpowiedź: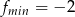 ,
, 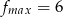
- Najdłuższym takim przedziałem jest przedział
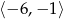 .
.
Odpowiedź: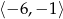
- Odczytujemy z wykresu (patrzymy kiedy wykres jest poniżej prostej
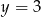 ).
).
Odpowiedź: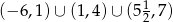
- Równanie
![[f(x)]2 = 4](https://img.zadania.info/zad/3151872/HzadR6x.gif) oznacza, że
oznacza, że 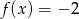 lub
lub 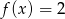 . Z podanego wykresu wynika, że pierwsze z tych równań ma jedno rozwiązanie a drugie ma ich 6.
. Z podanego wykresu wynika, że pierwsze z tych równań ma jedno rozwiązanie a drugie ma ich 6.
Odpowiedź: W 7 punktach

