Zadanie nr 4095952
Na rysunku przedstawiono wykres funkcji 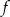 .
.
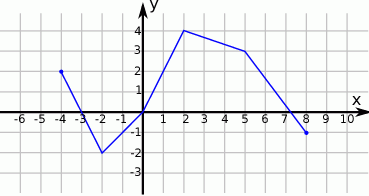
Odczytaj z wykresu i zapisz:
- maksymalne przedziały monotoniczności funkcji
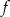 ,
, - liczbę rozwiązań równania
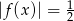 .
.
Rozwiązanie
- Odczytujemy z wykresu. Funkcja jest malejąca na przedziałach:
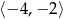 i
i 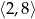 . Funkcja jest rosnąca na przedziale:
. Funkcja jest rosnąca na przedziale: 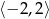
Odpowiedź: Malejąca na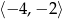 i
i 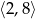 . Rosnąca na
. Rosnąca na 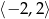 .
. -
Sposób I
Szkicujemy wykres
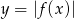 (odbijamy część wykresu
(odbijamy część wykresu 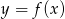 znajdującą się poniżej osi
znajdującą się poniżej osi 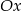 do góry).
do góry). 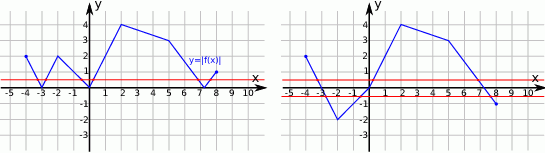
Widać teraz, że wykres
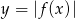 przecina prostą
przecina prostą 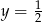 w 6 punktach.
w 6 punktach. Sposób II
Jeżeli
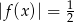 to
to 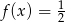 lub
lub 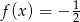 . Rysujemy na wykresie
. Rysujemy na wykresie 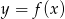 proste
proste 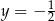 i
i 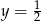 . Z wykresu widać, że są 3 liczby
. Z wykresu widać, że są 3 liczby  spełniające równanie
spełniające równanie 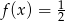 i 3 liczby
i 3 liczby  spełniające
spełniające 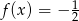 .
.
Odpowiedź: 6

