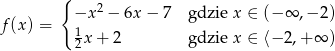/Szkoła średnia/Funkcje - wykresy/Dany wykres

Zadanie nr 7356119

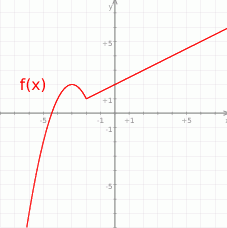
Na rysunku przedstawiony jest wykres pewnej funkcji o wzorze

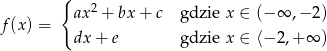
{ 2 f (x) = ax + bx+ c gdzie x ∈ (− ∞ ,− 2) dx + e gdzie x ∈ ⟨− 2,+ ∞ )

PIC

  • Dla jakich argumentów x spełniona jest nierówność f(x) ≥ 2 ?
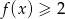  • Podaj przedziały, w których funkcja jest rosnąca.
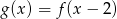  • Narysuj wykres funkcji g(x) = f(x − 2) .
  • Napisz wzór funkcji f .
Wersja PDF

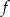Rozwiązanie

  • Sprawdzamy na wykresie, kiedy wartości funkcji są nie mniejsze niż 2.  
    Odpowiedź: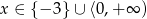 x ∈ { −3 }∪ ⟨0 ,+ ∞ )
  • Odczytujemy z wykresu.  
    Odpowiedź: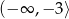 (− ∞ ,− 3⟩ i ⟨− 2,+ ∞ )
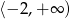
  • Musimy przesunąć wykres funkcji 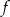f o dwie jednostki w prawo.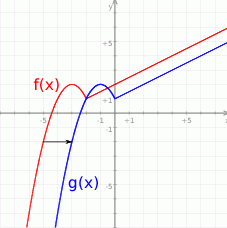
    PIC
  • Najpierw zajmijmy się lewą częścią wzoru, czyli parabolą. Ma ona wierzchołek w punkcie 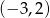(− 3,2) , czyli jest postaci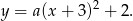
    2 y = a(x + 3) + 2.

    Wiemy ponadto, że przechodzi przez punkt 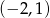(− 2,1) . Z tego obliczamy a .

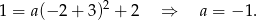
    2 1 = a(− 2 + 3) + 2 ⇒ a = − 1.

    Jest to więc funkcja

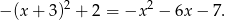
    2 2 − (x + 3) + 2 = −x − 6x − 7.

    Teraz zajmijmy się prawą stroną, czyli funkcją liniową. Wiemy, że przechodzi ona przez punkt 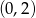(0,2) , czyli jest postaci 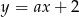y = ax + 2 . Współczynnik a obliczamy z tego, że przechodzi przez punkt (− 2,1) .

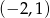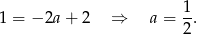
    1 = − 2a + 2 ⇒ a = 1-. 2

    Zatem funkcja 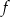f ma wzór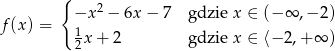

    { 2 f(x) = −x − 6x − 7 gdzie x ∈ (− ∞ ,− 2) 12x + 2 gdzie x ∈ ⟨− 2,+ ∞ )

     
    Odpowiedź: { 2 f(x) = −x − 6x − 7 gdzie x ∈ (− ∞ ,− 2) 12x + 2 gdzie x ∈ ⟨− 2,+ ∞ )

Wersja PDF