Zadanie nr 9082363
Na poniższym rysunku przedstawiono wykres funkcji 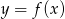 .
.
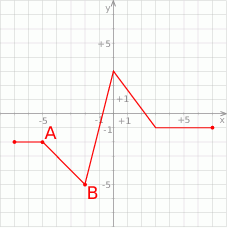
- Wyznacz zbiór wartości funkcji
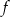 .
. - Oblicz
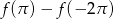 .
. - Rozwiąż równanie
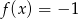 .
. - Napisz równanie prostej
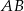 .
.
Rozwiązanie
- Odczytujemy z wykresu.
Odpowiedź: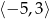
- Ponieważ
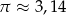 i
i 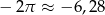 mamy
mamy 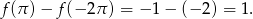
Odpowiedź: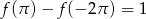
- Odczytujemy z wykresu.
Odpowiedź: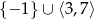
-
Sposób I
Szukamy prostej postaci
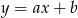 . Wstawiając do tego równania współrzędne punktów
. Wstawiając do tego równania współrzędne punktów 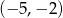 i
i 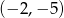 mamy
mamy 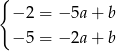
Odejmując od drugiego równania pierwsze (żeby skrócić
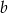 ) mamy
) mamy 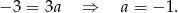
Stąd
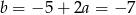 .
. Sposób II
Możemy też skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty
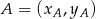 i
i 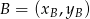 :
: 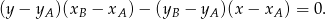
W naszej sytuacji mamy
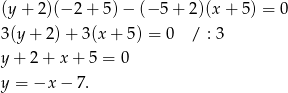
Odpowiedź: