/Szkoła średnia/Funkcje - wykresy/Dany wykres

Zadanie nr 9130751

Dodaj do ulubionych
Dodaj do rozwiązanych

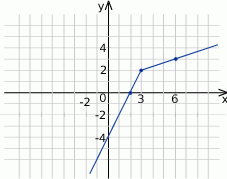
Dany jest wykres funkcji 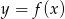y = f (x) , której dziedziną jest zbiór liczb rzeczywistych.

  • Wyznacz wzór tej funkcji korzystając z danych na rysunku.
  • Określ monotoniczność funkcji f.
  • Napisz, jaką najmniejszą wartość przyjmuje funkcja 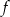f dla argumentów należących do przedziału ⟨1;6⟩ .
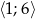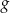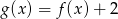  • Narysuj wykres funkcji g określonej wzorem: g (x) = f(x )+ 2 .
PIC

Rozwiązanie

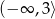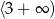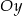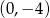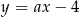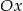  • Z wykresu widać, że funkcja będzie miała inny wzór na przedziale (− ∞ ,3⟩ a inny na ⟨3 + ∞ ) . Jeżeli chodzi o pierwszy przedział, to na nim jest to funkcja liniowa, która przecina oś Oy w punkcie (0,− 4) , jest więc postaci y = ax− 4 . Współczynnik a wyznaczamy z faktu, że wykres ten przecina oś Ox w punkcie 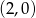(2,0) . Zatem
    0 = 2a− 4 ⇒ a = 2.

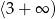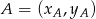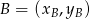    Teraz zajmijmy się funkcją na przedziale ⟨3+ ∞ ) . Aby napisać wzór tej funkcji skorzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA) i B = (xB,yB ) :

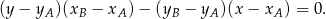
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    W naszej sytuacji 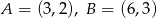A = (3,2 ), B = (6,3) oraz

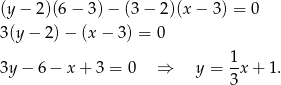
    (y − 2)(6 − 3) − (3 − 2)(x − 3) = 0 3(y − 2 )− (x − 3 ) = 0 1- 3y − 6 − x + 3 = 0 ⇒ y = 3x + 1.

    Zatem wzór funkcji jest następujący

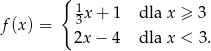
    { 1 3x + 1 dla x ≥ 3 f(x ) = 2x − 4 dla x < 3.

     
    Odpowiedź: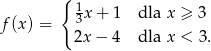 { 1 f(x ) = 3x + 1 dla x ≥ 3 2x − 4 dla x < 3.

  • Z wykresu widzimy, że funkcja jest rosnąca.  
    Odpowiedź: Rosnąca.
  • Odczytujemy z wykresu: f(1) = − 2 .  
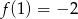    Odpowiedź: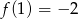 f(1) = − 2
  • Wykres funkcji 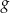g powstaje z wykresu funkcji 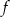f przez przesunięcie o dwie jednostki w górę.
    PIC
Wersja PDF