W trójkącie 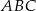 poprowadzono prostą
poprowadzono prostą 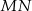 równoległą do prostej
równoległą do prostej 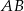 tak, że
tak, że 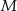 należy do
należy do 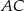 ,
, 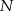 należy do
należy do 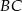 oraz
oraz 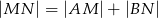 . Oblicz
. Oblicz 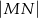 , jeśli
, jeśli 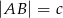 , a miary kątów trójkąta przy boku
, a miary kątów trójkąta przy boku 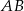 wynoszą
wynoszą  oraz
oraz 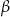 .
.
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Odcinki równoległe do boków
W trójkącie 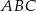 na boku
na boku 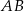 wybrano takie punkty
wybrano takie punkty 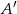 i
i 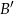 , że
, że
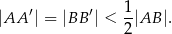
Przez punkty 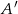 i
i 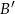 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 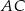 i
i 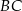 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 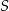 . Wykaż, że odcinek
. Wykaż, że odcinek 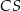 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 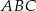 .
.
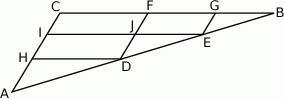
Odcinki 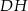 i
i 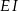 są równoległe do boku
są równoległe do boku 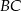 trójkąta
trójkąta 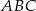 , a odcinki
, a odcinki 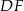 i
i 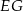 są równoległe do boku
są równoległe do boku 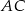 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 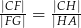 , to
, to 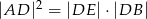 .
.