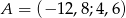/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków

Zadanie nr 1063370

Dodaj do ulubionych
Dodaj do rozwiązanych

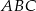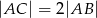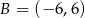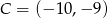W trójkącie ABC , gdzie |AC | = 2|AB | dane są B = (− 6,6) i C = (− 10,− 9) . Wyznacz współrzędne wierzchołka 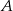A , jeżeli leży on na prostej 3y + x = 1 .

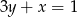Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

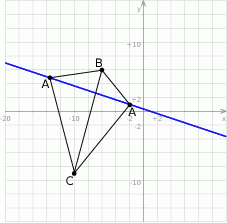
Jeżeli obrazek jest naprawdę szkicowy to niewiele z niego widać, więc zabieramy się do rachunków. Wiemy, że szukany punkt 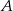A leży na prostej o równaniu 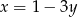x = 1 − 3y , więc ma on współrzędne postaci 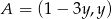A = (1 − 3y,y) . Aby wyliczyć 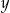y wystarczy skorzystać z podanej informacji: 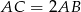AC = 2AB . Liczymy

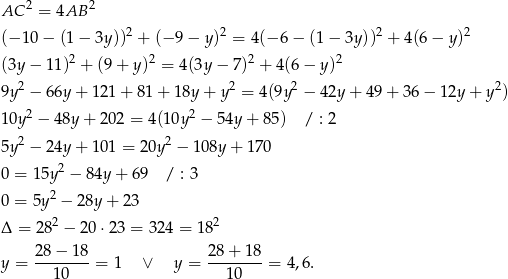
2 2 AC = 4AB (− 10 − (1 − 3y ))2 + (− 9 − y)2 = 4 (− 6 − (1 − 3y ))2 + 4(6 − y )2 2 2 2 2 (3y − 1 1) + (9 + y ) = 4(3y − 7) + 4(6− y) 9y 2 − 6 6y+ 121 + 81 + 18y + y2 = 4(9y2 − 42y + 49 + 36 − 12y + y2) 10y 2 − 48y+ 202 = 4 (10y2 − 54y + 85) / : 2 2 2 5y − 2 4y+ 101 = 20y − 1 08y + 170 0 = 15y2 − 84y + 69 / : 3 0 = 5y2 − 28y + 23 2 2 Δ = 28 − 20 ⋅23 = 3 24 = 18 28-−-18- 28+--18- y = 1 0 = 1 ∨ y = 10 = 4,6 .

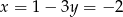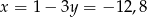Mamy wtedy odpowiednio x = 1− 3y = − 2 i x = 1− 3y = − 12,8 .  
Odpowiedź: 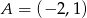A = (− 2,1) lub A = (− 12,8;4,6)

Wersja PDF