Zadanie nr 1980874
Znajdź taki punkt 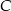 , leżący na prostej
, leżący na prostej 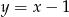 , aby pole trójkąta
, aby pole trójkąta 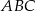 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 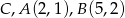 było równe 5.
było równe 5.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
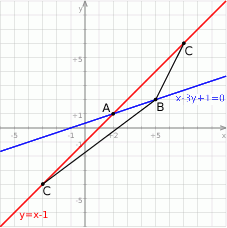
Z podanej informacji o równaniu prostej, na której leży punkt 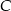 wiemy, że ma on współrzędne postaci
wiemy, że ma on współrzędne postaci 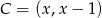 .
.
Sposób I
Korzystamy teraz ze wzoru na pole trójkąta o wierzchołkach 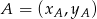 ,
, 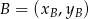 i
i 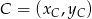 .
.
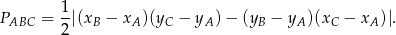
W naszej sytuacji mamy
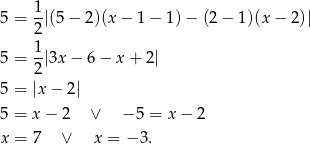
Zatem 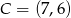 lub
lub 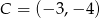 .
.
Sposób II
Tym razem obliczmy pole trójkąta wprost, ze wzoru 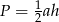 . Liczymy długość podstawy trójkąta
. Liczymy długość podstawy trójkąta
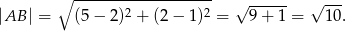
To pozwala obliczyć długość wysokości 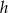 trójkąta
trójkąta 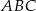 opuszczonej na bok
opuszczonej na bok 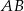 .
.
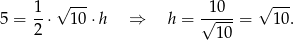
Teraz będziemy chcieli skorzystać ze wzoru na odległość punktu od prostej. Zanim to jednak zrobimy, napiszmy równanie prostej 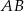 . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 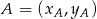 i
i 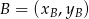 :
:
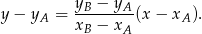
W naszej sytuacji mamy
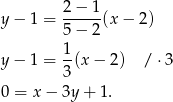
Wiemy, że punkt 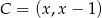 leży w odległości
leży w odległości 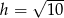 od prostej
od prostej 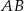 . Zapiszmy ten warunek korzystając ze wzoru na odległość punktu
. Zapiszmy ten warunek korzystając ze wzoru na odległość punktu 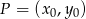 od prostej
od prostej 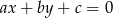 :
:
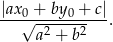
W naszej sytuacji mamy
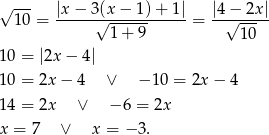
Zatem 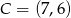 lub
lub 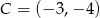 .
.
Odpowiedź: 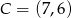 lub
lub