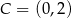/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków

Zadanie nr 2530142

Okrąg wpisany w trójkąt ABC jest opisany równaniem

2 2 x + y − 10x + 6y + 29 = 0.

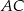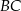Punkty styczności tego okręgu z bokami AC i BC trójkąta 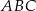ABC leżą na prostej o równaniu: 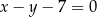x − y − 7 = 0 . Wyznacz współrzędne wierzchołka 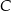C trójkąta ABC .

Wersja PDF

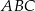Rozwiązanie

Przekształćmy najpierw równanie danego okręgu, tak aby ustalić jaki ma środek i promień

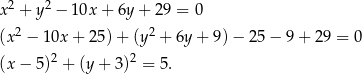
2 2 x + y − 10x + 6y + 2 9 = 0 (x2 − 10x + 25 )+ (y 2 + 6y + 9 )− 25 − 9 + 2 9 = 0 (x − 5)2 + (y+ 3)2 = 5.

Jest to zatem okrąg o środku 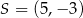S = (5,− 3) i promieniu 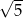√ -- 5 . Możemy zatem zrobić schematyczny rysunek.

PIC

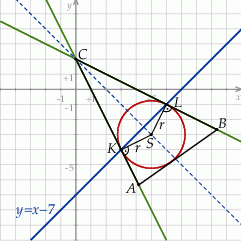
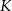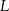Rozpocznijmy od wyznaczenia współrzędnych punktów K i L w których dana prosta przecina dany okrąg. Podstawiamy 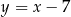y = x− 7 do równania okręgu.

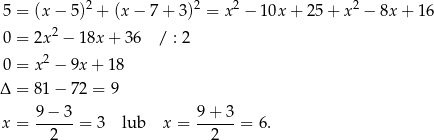
5 = (x− 5)2 + (x− 7+ 3)2 = x2 − 10x + 25 + x 2 − 8x + 16 2 0 = 2x − 18x + 36 / : 2 0 = x2 − 9x + 18 Δ = 81 − 72 = 9 9 − 3 9 + 3 x = ------= 3 lub x = ------= 6. 2 2

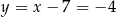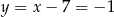Stąd y = x − 7 = − 4 i y = x − 7 = − 1 odpowiednio. Zatem 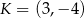K = (3,− 4) i L = (6,− 1) .

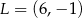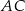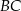Napiszemy teraz równania boków AC i BC trójkąta 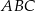ABC , czyli stycznych do okręgu w punktach 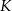K i L .

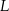Sposób I

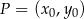
Skorzystamy ze wzoru na równanie prostej prostopadłej do wektora →v = [p,q] i przechodzącej przez punkt P = (x0,y0)

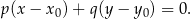
p(x − x0) + q(y − y0) = 0 .

W przypadku prostej 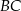BC bierzemy 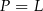P = L i

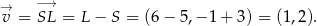
→v = −S→L = L − S = (6− 5,− 1+ 3) = (1,2).

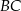Prosta BC ma więc równanie

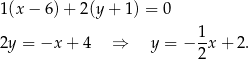
1(x − 6)+ 2(y + 1) = 0 2y = −x + 4 ⇒ y = − 1x + 2 . 2

Analogicznie wyznaczamy równanie prostej AC – jest to prosta przechodząca przez punkt P = K i prostopadła do wektora

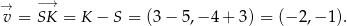
→v = −S→K = K − S = (3 − 5,− 4 + 3) = (− 2,− 1).

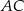Prosta AC ma więc równanie

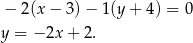
− 2(x− 3)− 1(y+ 4) = 0 y = − 2x + 2.

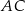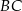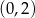Z otrzymanych równań prostych AC i BC widać, że przecinają oś Oy w tym samym punkcie (0,2) – musi to więc być ich punkt wspólny C .

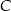Sposób II

Jeżeli nie chcemy używać wektorów, to mamy odrobinę więcej pomocniczych rachunków.

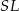Prosta BC jest prostopadła do prostej SL – zacznijmy od wyznaczenia współczynnika kierunkowego prostej 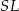SL . Jeżeli prosta ta ma równanie postaci 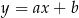y = ax+ b , to (podstawiamy współrzędne punktów 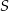S i L )

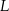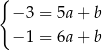
{ − 3 = 5a+ b − 1 = 6a+ b

Odejmujemy od drugiego równania pierwsze i mamy 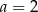a = 2 . Współczynnika 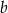b nie musimy wyznaczać, bo nie jest nam potrzebny. W takim razie prosta 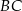BC , jako prostopadła do 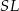SL , ma równanie postaci 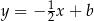y = − 1x + b 2 . Współczynnik 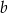b wyznaczamy podstawiając współrzędne punktu L .

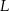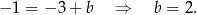
− 1 = −3 + b ⇒ b = 2.

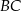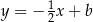Zatem prosta BC ma równanie: 1 y = − 2x+ b .

Dokładnie w ten sam sposób moglibyśmy wyznaczyć równanie drugiej stycznej – przechodzącej przez punkt 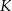K , ale zamiast tego napiszemy równanie prostej 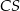CS . Jest ona prostopadła do danej prostej 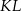KL , czyli ma równanie postaci 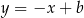y = −x + b oraz przechodzi przez punkt 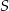S . Stąd

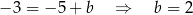
−3 = − 5+ b ⇒ b = 2

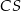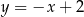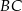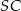i prosta CS ma równanie y = −x + 2 . Tak jak w poprzednim sposobie, zauważamy teraz, że proste BC i SC przecinają oś 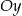Oy w tym samym punkcie C = (0,2) .  
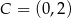Odpowiedź: C = (0,2)

Wersja PDF