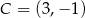Zadanie nr 2770019
W trójkącie  o polu 20 dane sa współrzędne dwóch wierzchołków:
o polu 20 dane sa współrzędne dwóch wierzchołków:  ,
, 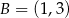 oraz środek
oraz środek 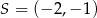 okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka
okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka 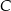 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
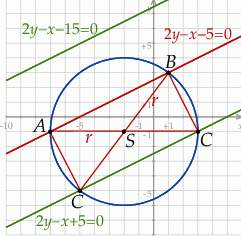
Zacznijmy od obliczenia rzeczy oczywistych: promienia  okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 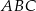
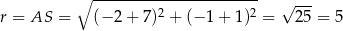
i długości odcinka 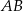
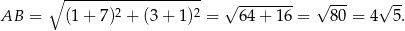
W szczególności, okrąg opisany na trójkącie 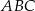 ma równanie
ma równanie
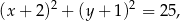
a wysokość trójkąta 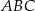 opuszczona na bok
opuszczona na bok 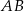 ma długość
ma długość
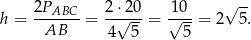
Napiszmy jeszcze równanie prostej 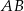 . Szukamy prostej w postaci
. Szukamy prostej w postaci 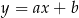 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 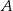 i
i 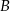 .
.
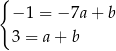
Odejmujemy od drugiego równania pierwsze i mamy 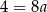 , czyli
, czyli 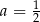 . Stąd
. Stąd 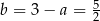 i prosta
i prosta 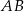 ma równanie
ma równanie
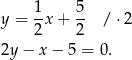
Szukamy teraz punktu 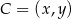 , którego odległość od prostej
, którego odległość od prostej 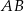 jest równa
jest równa 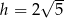 i który leży na danym okręgu. Zapiszmy najpierw warunek odległości od prostej
i który leży na danym okręgu. Zapiszmy najpierw warunek odległości od prostej 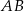
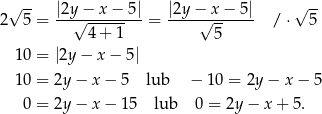
Otrzymane równania to równania dwóch prostych równoległych do prostych 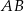 i odległych od niej o
i odległych od niej o 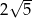 . Pozostało wyznaczyć punkty wspólne tych prostych z danym okręgiem. Jeżeli zrobiliśmy dość dokładny rysunek, to można zauważyć, że pierwsza z nich nie przecina okręgu. Można to sprawdzić rozwiązując odpowiednie równanie, ale można też sprawdzić, że odległość środka okręgu
. Pozostało wyznaczyć punkty wspólne tych prostych z danym okręgiem. Jeżeli zrobiliśmy dość dokładny rysunek, to można zauważyć, że pierwsza z nich nie przecina okręgu. Można to sprawdzić rozwiązując odpowiednie równanie, ale można też sprawdzić, że odległość środka okręgu 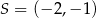 od tej prostej
od tej prostej
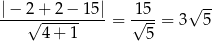
jest większa od promienia 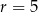 okręgu.
okręgu.
Pozostało znaleźć punkty wspólne drugiej prostej i okręgu. Podstawiamy 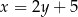 do równania okręgu.
do równania okręgu.
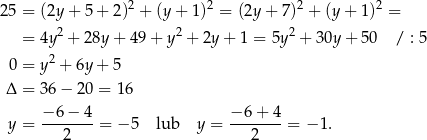
Stąd 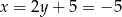 i
i 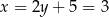 odpowiednio. Zatem
odpowiednio. Zatem 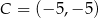 lub
lub 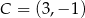 .
.
Odpowiedź: 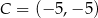 lub
lub