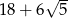Zadanie nr 6415120
Punkty 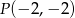 ,
, 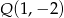 i
i 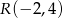 są środkami boków
są środkami boków 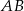 ,
, 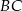 i
i 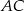 trójkąta
trójkąta 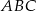 . Oblicz:
. Oblicz:
- Współrzędne wierzchołków trójkąta
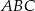 .
. - Obwód trójkąta
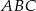 .
.
Rozwiązanie
-
Sposób I
Zacznijmy od szkicowego rysunku.
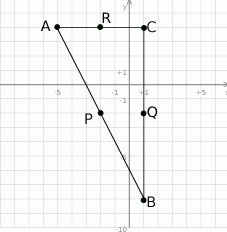
Niech
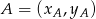 ,
, 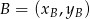 ,
, 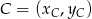 . Korzystając ze wzoru na współrzędne środka odcinka o końcach
. Korzystając ze wzoru na współrzędne środka odcinka o końcach 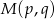 i
i 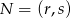
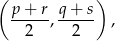
otrzymujemy zależności
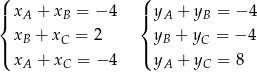
W każdym z układów, odejmujemy od pierwszego równania drugie i dodajemy trzecie. Otrzymamy
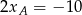 i
i 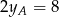 , czyli
, czyli 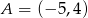 . Stąd już łatwo otrzymać
. Stąd już łatwo otrzymać 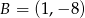 i
i 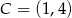 .
. Sposób II
Jak poprzednio, zacznijmy od rysunku.
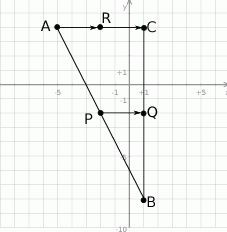
Ponieważ odcinek
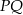 jest równoległy do boku
jest równoległy do boku 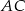 i jest od niego dwa razy krótszy, to
i jest od niego dwa razy krótszy, to 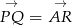 . To pozwala łatwo wyliczyć współrzędne punktu
. To pozwala łatwo wyliczyć współrzędne punktu 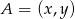 .
. ![→ PQ = [3,0] → AR = [− 2 − x,4 − y] → → PQ = AR [3 ,0] = [− 2 − x,4 − y ] ⇒ A = (x,y ) = (− 5,4).](https://img.zadania.info/zad/6415120/HzadR18x.gif)
Podobnie wyliczamy współrzędne pozostałych punktów.
Odpowiedź: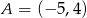 ,
, 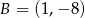 oraz
oraz 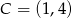
- Korzystając z poprzedniego podpunktu, możemy obliczyć długości boków danego trójkąta.
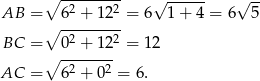
Obwód wynosi więc
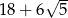 .
.
Odpowiedź: