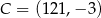Zadanie nr 6690986
Odległość każdego z wierzchołków 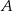 i
i 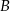 trójkąta
trójkąta 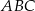 od punktu
od punktu 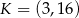 jest równa
jest równa 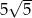 , a odległość tych wierzchołków od punktu
, a odległość tych wierzchołków od punktu 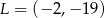 jest równa 25. Okrąg opisany na trójkącie
jest równa 25. Okrąg opisany na trójkącie 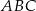 jest styczny do prostej
jest styczny do prostej 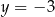 w punkcie
w punkcie 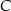 . Punkt
. Punkt 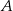 znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta
znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta 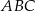 .
.
Rozwiązanie
Treść jest dość skomplikowana, więc zaczynamy od schematycznego rysunku.
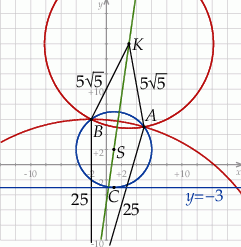
Zapiszmy najpierw informację o odległościach punktów 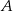 i
i 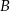 od punktów
od punktów 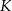 i
i 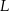 . Jeżeli oznaczmy przez
. Jeżeli oznaczmy przez 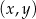 współrzędne któregokolwiek z punktów
współrzędne któregokolwiek z punktów 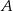 i
i 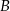 , to mamy
, to mamy
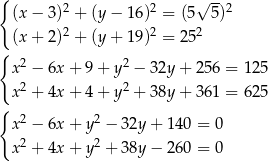
Odejmujemy od drugiego równania pierwsze i mamy
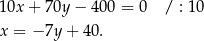
Podstawiamy to wyrażenie do drugiego równania układu
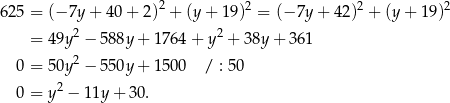
Rozwiązujemy otrzymane równanie kwadratowe.
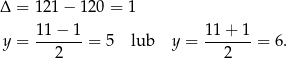
Stąd 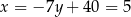 i
i 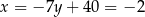 odpowiednio. Zatem
odpowiednio. Zatem 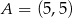 i
i 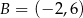 .
.
Teraz czas na zapisanie informacji o styczności okręgu opisanego na trójkącie 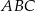 do prostej
do prostej 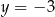 . Jeżeli oznaczymy przez
. Jeżeli oznaczymy przez 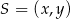 środek tego okręgu, to jego promień jest równy
środek tego okręgu, to jego promień jest równy 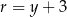 . Wiemy też, że
. Wiemy też, że 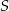 leży na symetralnej boku
leży na symetralnej boku 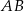 . Otrzymujemy więc układ równań
. Otrzymujemy więc układ równań
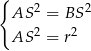
Zajmijmy się najpierw pierwszym równaniem, tzn. wyznaczmy równanie symetralnej odcinka 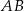 .
.
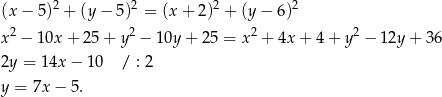
W takim razie drugie równanie przyjmuje postać
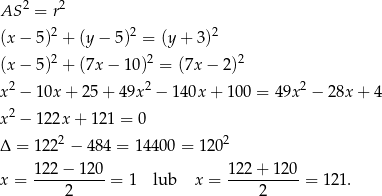
Stąd 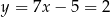 lub
lub 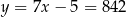 . Zatem
. Zatem 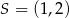 lub
lub 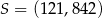 , czyli
, czyli 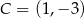 lub
lub 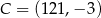 . Drugą możliwość może być trudno sobie wyobrazić – tak to mniej więcej wygląda po przeskalowaniu.
. Drugą możliwość może być trudno sobie wyobrazić – tak to mniej więcej wygląda po przeskalowaniu.
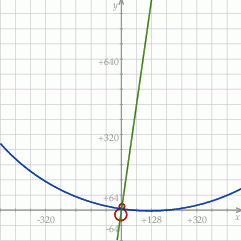
Odpowiedź: 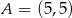 ,
, 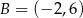 ,
, 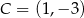 lub
lub