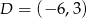Zadanie nr 7302070
Wierzchołek 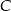 trójkąta ostrokątnego
trójkąta ostrokątnego 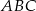 ma współrzędne
ma współrzędne 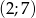 . Prosta o równaniu
. Prosta o równaniu 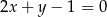 jest symetralną wysokości
jest symetralną wysokości 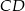 , a prosta o równaniu
, a prosta o równaniu 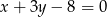 zawiera środkową trójkąta poprowadzoną z wierzchołka
zawiera środkową trójkąta poprowadzoną z wierzchołka 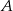 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 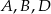 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
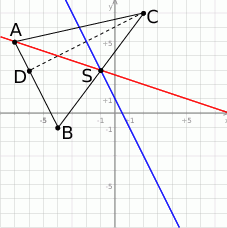
Po pierwsze zauważmy, że punkt 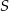 przecięcia się danych prostych, to dokładnie środek boku
przecięcia się danych prostych, to dokładnie środek boku 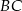 szukanego trójkąta (bo środek boku leży na każdej z opisanych prostych). Wyliczmy jego współrzędne (wstawiamy
szukanego trójkąta (bo środek boku leży na każdej z opisanych prostych). Wyliczmy jego współrzędne (wstawiamy  -a z drugiego równania do pierwszego).
-a z drugiego równania do pierwszego).
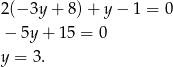
Zatem 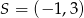 . Teraz łatwo wyliczyć współrzędne punktu
. Teraz łatwo wyliczyć współrzędne punktu 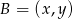
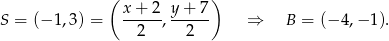
Wiemy, że prosta 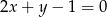 jest prostopadła do wysokości opuszczonej na bok
jest prostopadła do wysokości opuszczonej na bok 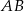 , jest ona więc równoległa do tego boku. Napiszemy teraz równanie prostej równoległej do tej prostej i przechodzącej przez punkt
, jest ona więc równoległa do tego boku. Napiszemy teraz równanie prostej równoległej do tej prostej i przechodzącej przez punkt 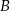 (będzie to więc prosta
(będzie to więc prosta 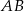 ). Otrzymaną prostą przetniemy z podaną środkową
). Otrzymaną prostą przetniemy z podaną środkową 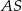 i w ten sposób otrzymamy punkt
i w ten sposób otrzymamy punkt 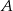 .
.
Liczymy, prosta 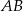 jest postaci
jest postaci 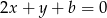 ,
, 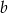 wyliczamy z faktu, że należy do niej punkt
wyliczamy z faktu, że należy do niej punkt 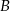 .
.
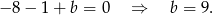
Szukamy teraz punktu 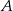 , czyli punktu przecięcia sie prostych
, czyli punktu przecięcia sie prostych 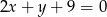 i
i 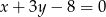 . Od razu podstawiamy za
. Od razu podstawiamy za  z drugiego równania do pierwszego.
z drugiego równania do pierwszego.
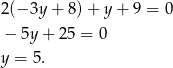
Stąd 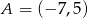 .
.
Aby wyliczyć współrzędne punktu 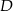 , napiszmy równanie prostej prostopadłej do
, napiszmy równanie prostej prostopadłej do 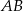 i przechodzącej przez punkt
i przechodzącej przez punkt 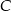 . Najprościej jest skorzystać ze wzoru na równanie prostej prostopadłej do wektora
. Najprościej jest skorzystać ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/7302070/HzadR28x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 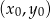
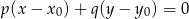
W naszej sytuacji ![→ → v = AB = [3,− 6]](https://img.zadania.info/zad/7302070/HzadR31x.gif) i
i 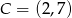 Prosta
Prosta  ma więc równanie
ma więc równanie
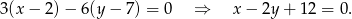
Pozostało znaleźć jej punkt wspólny z prostą 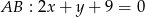 . Od razu podstawiamy za
. Od razu podstawiamy za 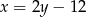 w równaniu prostej
w równaniu prostej 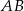 .
.
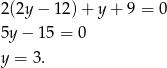
Stąd 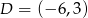 .
.
Odpowiedź: 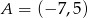 ,
, 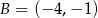 ,
,