/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków

Zadanie nr 8961042

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwa wierzchołki trójkąta 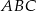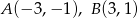ABC : A(− 3 ,− 1 ), B (3,1) . Punkt 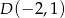D (−2 ,1) należy do boku 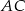AC , a odcinek 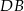DB jest środkową w trójkącie 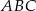ABC . Oblicz:

  • współrzędne wierzchołka C ;
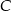  • pole trójkąta ABC .

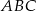Rozwiązanie

  • Zaczynamy od rysunku.
    PIC

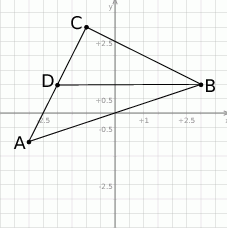
    Ponieważ punkt 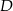D jest środkiem odcinka 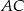AC , współrzędne punktu 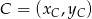C = (xC,yC ) muszą spełniać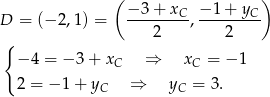

    ( − 3 + xC − 1+ yC ) D = (− 2,1) = ---------,--------- { 2 2 − 4 = − 3 + xC ⇒ xC = − 1 2 = − 1 + yC ⇒ yC = 3.

    Zatem C = (− 1,3) .  
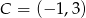    Odpowiedź: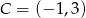 C = (− 1,3 )

  • Jeżeli zaznaczymy wierzchołek 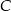C w układzie współrzędnych, to wydaje się, że trójkąt 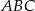ABC jest prostokątny. Sprawdźmy czy tak jest.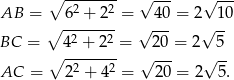
    ∘ ------- √ --- √ --- AB = 6 2 + 22 = 40 = 2 10 ∘ -2----2 √ --- √ -- BC = ∘ 4--+-2--= 2 0 = 2 5 AC = 22 + 4 2 = √ 20-= 2√ 5-.

    Mamy więc

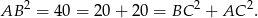
    2 2 2 AB = 4 0 = 20 + 20 = BC + AC .

    Zatem trójkąt 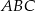ABC istotnie jest prostokątny i jego pole jest równe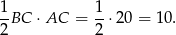

    1- 1- 2BC ⋅ AC = 2 ⋅2 0 = 10.

     
    Odpowiedź: 10

Wersja PDF