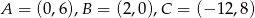Zadanie nr 9105212
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 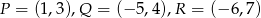 .
.
Rozwiązanie
Powiedzmy, że punkty 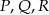 są odpowiednio środkami boków
są odpowiednio środkami boków 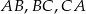 trójkąta
trójkąta 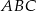 .
.
Sposób I
Jeżeli oznaczymy szukane punkty przez 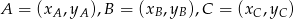 to ze wzoru na współrzędne środka odcinka mamy układ równań
to ze wzoru na współrzędne środka odcinka mamy układ równań
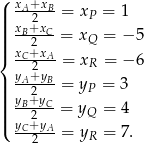
Daje to nam dwa układy
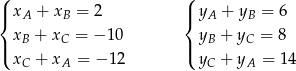
Rozwiązujemy te układy. Z pierwszych równań mamy 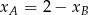 oraz
oraz 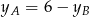 . Podstawiamy te wyrażenia do trzecich równań i mamy układy
. Podstawiamy te wyrażenia do trzecich równań i mamy układy
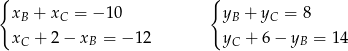
Dodając teraz równania stronami otrzymujemy 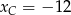 oraz
oraz 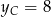 . Stąd
. Stąd 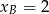 i
i 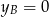 oraz
oraz 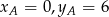 .
.
Sposób II
Zadanie można też dość szybko rozwiązać używając wektorów.
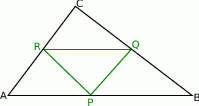
Jeżeli naszkicujemy trójkąt  z zaznaczonymi środkami boków to ponieważ odcinek łączący środki boków trójkąta jest równoległy do odpowiedniego boku oraz ma długość równą połowie długości tego boku, mamy
z zaznaczonymi środkami boków to ponieważ odcinek łączący środki boków trójkąta jest równoległy do odpowiedniego boku oraz ma długość równą połowie długości tego boku, mamy
![−→ −→ −→ AP = PB = RQ = [1,− 3] −→ −→ RC = P Q = [− 6,1].](https://img.zadania.info/zad/9105212/HzadR16x.gif)
Równości te pozwalają wyliczyć współrzędne punktów  .
.
![−→ AP = [1− xA,3 − yA ] = [1 ,− 3 ] ⇒ A = (0 ,6 ) −→ P B = [xB − 1,yB − 3] = [1,− 3] ⇒ B = (2,0) −→ RC = [x + 6,y − 7] = [− 6,1] ⇒ C = (− 12,8). C C](https://img.zadania.info/zad/9105212/HzadR18x.gif)
Na koniec obrazek dla ciekawskich.
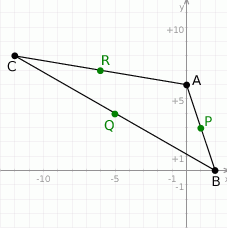
Odpowiedź: