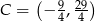/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków

Zadanie nr 9506459

Dodaj do ulubionych
Dodaj do rozwiązanych

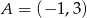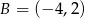Dane są punkty A = (− 1,3) i B = (− 4,2) . Wyznacz współrzędne punktu 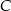C na prostej 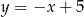y = −x + 5 tak, aby pole trójkąta 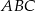ABC było równe 7.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

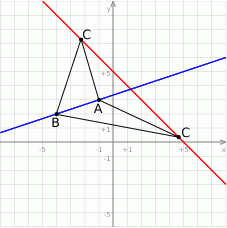
Sposób I

Obliczmy długość podstawy trójkąta 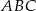ABC

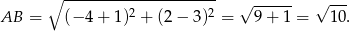
∘ --------------------- √ ------ √ --- AB = (− 4+ 1)2 + (2− 3 )2 = 9+ 1 = 10.

Z podanego pola obliczamy jaka jest długość wysokości opuszczonej na bok 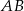AB .

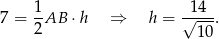
1 14 7 = -AB ⋅h ⇒ h = √---. 2 10

Co dalej? – szukamy punktu 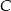C na danej prostej, który jest w odległości 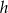h od prostej AB .

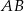Napiszmy najpierw równanie prostej 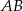AB . Można to zrobić korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale my zrobimy to wprost: szukamy prostej w postaci 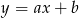y = ax + b . Podstawiamy współrzędne punktów 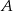A i B .

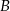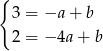
{ 3 = −a + b 2 = − 4a + b

Odejmujemy od pierwszego równania drugie (żeby skrócić b ) i mamy

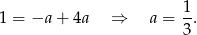
1- 1 = −a + 4a ⇒ a = 3.

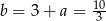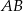Zatem b = 3 + a = 130 i prosta AB ma równanie:

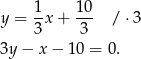
y = 1x + 10- / ⋅3 3 3 3y − x − 10 = 0.

Sprawdzamy teraz, kiedy odległość punktu 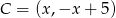C = (x,−x + 5) od prostej 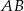AB jest równa h .

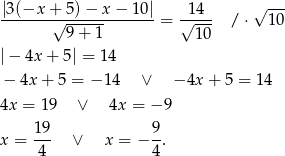
|3 (−x + 5)− x − 10| 14 √ --- -------√-------------= √---- / ⋅ 10 9+ 1 10 |− 4x + 5| = 14 − 4x + 5 = − 14 ∨ − 4x + 5 = 14 4x = 19 ∨ 4x = − 9 x = 19- ∨ x = − 9-. 4 4

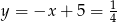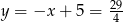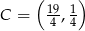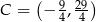Wtedy 1 y = −x + 5 = 4 i 29 y = −x + 5 = 4 odpowiednio. Zatem ( 19 1) C = 4 ,4 lub C = (− 9, 29) 4 4 .

Sposób II

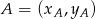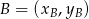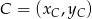Korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

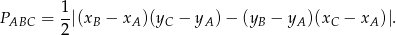
1 PABC = 2-|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|.

W naszej sytuacji 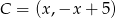C = (x,−x + 5) , więc mamy równanie

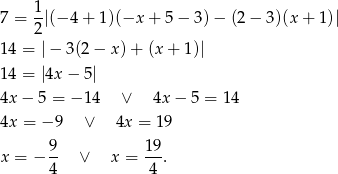
1- 7 = 2 |(− 4 + 1)(−x + 5 − 3) − (2 − 3)(x + 1)| 14 = |− 3(2− x) + (x + 1)| 14 = |4x − 5| 4x − 5 = − 14 ∨ 4x− 5 = 14 4x = − 9 ∨ 4x = 19 9 19 x = − -- ∨ x = --. 4 4

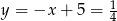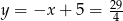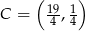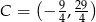Wtedy y = −x + 5 = 1 4 i y = −x + 5 = 29 4 odpowiednio. Zatem ( ) C = 19, 1 4 4 lub ( ) C = − 94, 294 .  
Odpowiedź: 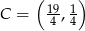( 19- 1) C = 4 , 4 lub ( 9 29) C = − 4,4

Wersja PDF