Zadanie nr 1066117
Dla jakich liczb całkowitych dodatnich 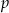 liczby
liczby 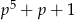 i
i 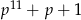 są pierwsze.
są pierwsze.
Rozwiązanie
Zauważmy, że
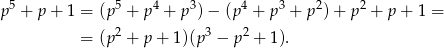
Podobnie
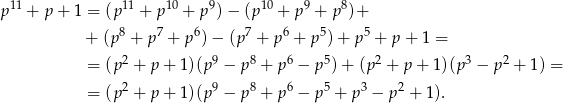
Jak wpaść na te rozkłady? – moim zdaniem najprościej jest policzyć największy wspólny dzielnik liczb 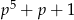 i
i 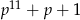 używając algorytmu Euklidesa. Jak się to zrobi to wyjdzie
używając algorytmu Euklidesa. Jak się to zrobi to wyjdzie 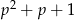 . A jak wiemy, że oba wielomiany dzielą się przez
. A jak wiemy, że oba wielomiany dzielą się przez 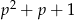 to napisanie rozkładów jest już automatyczne.
to napisanie rozkładów jest już automatyczne.
Ponieważ 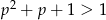 , obie liczby będą pierwsze tylko dla
, obie liczby będą pierwsze tylko dla
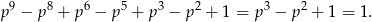
To jest jednak możliwe tylko dla 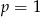 .
.
Odpowiedź: