/Konkursy/Zadania/Liczby/Całkowite

Zadanie nr 2648400

Znajdź liczbę doskonałą, która jest podzielna przez 4 i ma dokładnie 6 dzielników.

Wersja PDF

Rozwiązanie

Liczba doskonała to taka, która jest równa sumie swoich dzielników, które są od niej mniejsze.

Sposób I

Jeżeli oznaczymy szukaną liczbę przez n , to ponieważ wiemy, że dzieli się przez 4, możemy wypisać kilka jej dzielników:

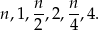
n n n,1 ,-,2, -,4. 2 4

Łatwo sprawdzić, że każde dwie z tych liczb muszą być różne, więc skoro jest ich 6, to muszą to być wszystkie dzielniki. Mamy więc równanie (z doskonałości)

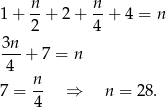
n n 1+ --+ 2 + --+ 4 = n 2 4 3n-+ 7 = n 4 7 = n- ⇒ n = 2 8. 4

Sposób II

Możemy też skorzystać z następującej charakteryzacji parzystych liczb doskonałych: każda taka liczba jest postaci 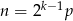n = 2k− 1p , gdzie 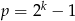p = 2k − 1 jest liczbą pierwszą (są to tzw. liczby pierwsze Mersenne’a). Na mocy tej charakteryzacji, wszystkie dzielniki parzystej liczby doskonałej to

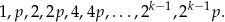
k−1 k− 1 1,p,2,2p,4 ,4p ,...,2 ,2 p.

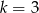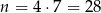Skoro dzielników ma być 6, to musi być k = 3 . Zatem n = 4 ⋅7 = 2 8 .  
Odpowiedź: 28

Wersja PDF