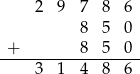Zadanie nr 4901966
Odgadnij jakie cyfry kryją się za literami w podanym działaniu, jeżeli różnym literom odpowiadają różne cyfry.

Rozwiązanie
Patrzymy najpierw na cyfry jedności. Ponieważ dodanie do 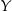
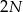 ma nie zmieniać cyfry jedności, musi być
ma nie zmieniać cyfry jedności, musi być 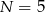 lub
lub 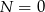 . Jeżeli
. Jeżeli 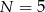 to dodawanie
to dodawanie 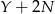 daje przeniesienie 1 na cyfrę dziesiątek. Patrząc na cyfrę dziesiątek, mamy znowu
daje przeniesienie 1 na cyfrę dziesiątek. Patrząc na cyfrę dziesiątek, mamy znowu 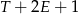 (1 z przeniesienia!) ma dwać
(1 z przeniesienia!) ma dwać 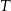 , czyli cyfrą jedności
, czyli cyfrą jedności 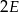 musi być 9, a to nie jest możliwe. Zatem musi być
musi być 9, a to nie jest możliwe. Zatem musi być 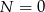 i nie ma przeniesienia na cyfrę dziesiątek.
i nie ma przeniesienia na cyfrę dziesiątek.
Patrząc teraz na cyfrę dziesiątek, mamy podobnie jak wcześniej 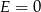 lub
lub 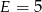 . Ponieważ różnym literom odpowiadają różne cyfry, mamy
. Ponieważ różnym literom odpowiadają różne cyfry, mamy 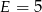 i mamy przeniesienie 1 na cyfrę setek. Ponieważ cyfry tysięcy i dziesiątek tysięcy pierwszej liczby i wyniku są różne, więc musi być przeniesienie na te pozycje. Gdyby na cyfrę tysięcy było przeniesienie 1, to musiałoby być
i mamy przeniesienie 1 na cyfrę setek. Ponieważ cyfry tysięcy i dziesiątek tysięcy pierwszej liczby i wyniku są różne, więc musi być przeniesienie na te pozycje. Gdyby na cyfrę tysięcy było przeniesienie 1, to musiałoby być 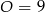 i
i 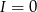 , co nie jest możliwe, bo
, co nie jest możliwe, bo 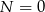 . Zatem na cyfrę tysięcy musi być przeniesienie 2 i
. Zatem na cyfrę tysięcy musi być przeniesienie 2 i 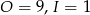 .
.
Żeby się nie pogubić zapiszmy co mamy do tej pory.
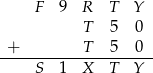
Popatrzmy teraz na cyfry setek. Mają one dawać przeniesienie 2, więc musi tam być 8 (bo 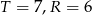 daje
daje 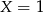 , a
, a 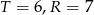 daje
daje 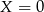 ). Jeżeli
). Jeżeli 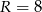 to
to 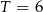 daje
daje 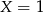 , co nie jest możliwe. Zatem
, co nie jest możliwe. Zatem 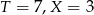 . Wtedy nie da się dobrać
. Wtedy nie da się dobrać 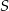 i
i 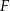 tak, żeby
tak, żeby 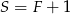 .
.
Zatem 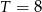 . Łatwo wtedy zobaczyć, że
. Łatwo wtedy zobaczyć, że 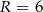 lub
lub 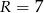 . Daje to nam układy
. Daje to nam układy
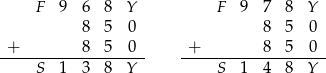
Łatwo zobaczyć, że w pierwszej sytuacji nie da się dobrać 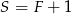 , a drugiej
, a drugiej 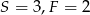 i mamy rozwiązanie
i mamy rozwiązanie