Zadanie nr 5469630
Suma cyfr pewnej liczby dwucyfrowej wynosi 12. Jeżeli od liczby utworzonej z przestawienia cyfr liczby początkowej odejemiemy 8 to otrzymamy liczbę 3 razy mniejszą od liczby początkowej. Znajdz tę liczbę.
Rozwiązanie
Oznaczmy wyjściową liczbę przez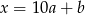 
(
i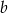 
- to odpowiednio cyfry dziesiątek i jedności). Liczba powstała przez przestawienie cyfr to 
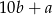. Mamy zatem równanie
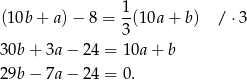
Pozostało skorzystać z podanej sumy cyfr: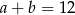 
.
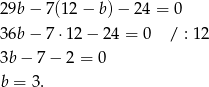
Stąd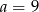 
.
Odpowiedź: 93
