Zadanie nr 7047543
W kryptogramie różnym literom odpowiadają różne cyfry. Podaj rozwiązanie.
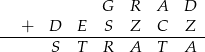
Rozwiązanie
Patrzymy najpierw na cyfry stek tysięcy ponieważ przy dodawaniu 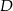 zamienia się na
zamienia się na 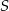 musi tam być przeniesienie. Zatem przeniesienie musi też być na poprzedniej cyfrze. Ponieważ największe możliwe przeniesienie to 1, więc musi być
musi tam być przeniesienie. Zatem przeniesienie musi też być na poprzedniej cyfrze. Ponieważ największe możliwe przeniesienie to 1, więc musi być 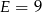 i
i 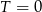 ,
, 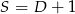 . Mamy zatem kryptogram
. Mamy zatem kryptogram
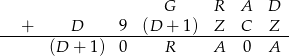
Jeżeli popatrzymy na cyfry jedności i setek, to oba dodawania 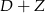 i
i 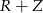 muszą dawać tę samą liczbę. Musi być zatem
muszą dawać tę samą liczbę. Musi być zatem 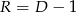 i na cyfrze setek jest przeniesienie. Ponadto na cyfrze tysięcy nie ma przeniesienia. Mamy zatem kryptogram
i na cyfrze setek jest przeniesienie. Ponadto na cyfrze tysięcy nie ma przeniesienia. Mamy zatem kryptogram
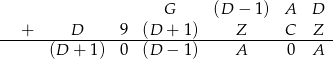
Ponieważ na cyfrze tysięcy nie ma przeniesienia, musi być 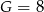 i mamy kryptogram
i mamy kryptogram
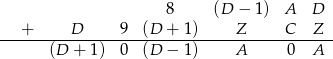
Popatrzmy teraz na cyfrę dziesiątek. Ma być 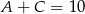 zatem
zatem 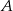 i
i 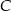 są równe 6 i 4 lub 7 i 3 (w pewnej kolejności). W pierwszej sytuacji musi być
są równe 6 i 4 lub 7 i 3 (w pewnej kolejności). W pierwszej sytuacji musi być 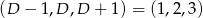 i mamy kryptogram
i mamy kryptogram
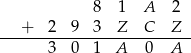
To jednak jest niemożliwe, bo jak poptrzymy cyfrę jedności, to zarówno 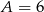 jak i
jak i 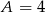 prowadzi do sprzeczności (nie da się dobrać
prowadzi do sprzeczności (nie da się dobrać 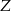 ).
).
Zatem 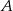 i
i 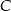 są równe 7 i 3 (w pewnej kolejności. Wtedy
są równe 7 i 3 (w pewnej kolejności. Wtedy 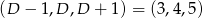 lub
lub 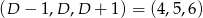 . Daje to nam kryptogramy
. Daje to nam kryptogramy
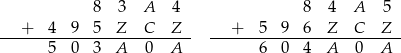
W pierwszym kryptogramie nie da się dobrać 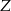 (patrzymy na jedności), a drugim musi być
(patrzymy na jedności), a drugim musi być 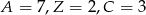 . Daje to odpowiedź:
. Daje to odpowiedź: