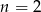/Konkursy/Zadania/Liczby/Całkowite

Zadanie nr 7128830

Dla jakich n należących do zbioru liczb naturalnych liczba 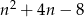2 n + 4n − 8 jest kwadratem liczby naturalnej?

Wersja PDF

Rozwiązanie

Mamy

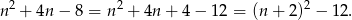
2 2 2 n + 4n − 8 = n + 4n+ 4− 12 = (n + 2 ) − 12 .

Jeżeli liczba ta ma być kwadratem to jest to co najwyżej 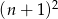2 (n + 1) (bo wyżej jest napisane, że na pewno jest mniejsza od 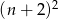(n + 2)2 ), czyli

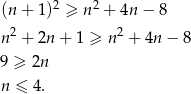
2 2 (n + 1) ≥ n + 4n − 8 2 2 n + 2n + 1 ≥ n + 4n − 8 9 ≥ 2n n ≤ 4 .

Łatwo sprawdzić, że tylko dla 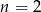n = 2 jest to kwadrat.  
Odpowiedź: n = 2

Wersja PDF