/Konkursy/Zadania/Liczby/Całkowite

Zadanie nr 9319843

Dodaj do ulubionych
Dodaj do rozwiązanych

Czy liczba nieparzysta i połowa następującej po niej liczby parzystej mogą mieć wspólny dzielnik większy niż 1?

Rozwiązanie

Jeżeli 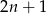2n + 1 jest taką liczbą nieparzystą, to połowa kolejnej liczby to n+ 1 .

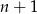Sposób I

Skorzystamy teraz z bardzo wygodnego faktu (jest to tak naprawdę algorytm Euklidesa)

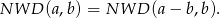
NW D (a,b) = NW D(a − b,b ).

W naszej sytuacji mamy

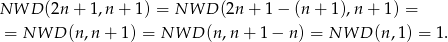
NW D (2n + 1,n + 1) = NW D (2n + 1− (n+ 1),n+ 1) = = NW D (n,n + 1) = NW D(n ,n+ 1− n) = NW D(n ,1) = 1.

Zatem liczby te są względnie pierwsze.

Sposób II

Ponieważ

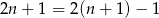
2n + 1 = 2(n+ 1)− 1

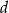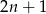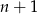Jeżeli jakaś liczba naturalna d dzieli jednocześnie 2n + 1 i n+ 1 , to musi dzielić -1, czyli d = 1 .  
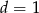Odpowiedź: Nie, liczby są względnie pierwsze.

Wersja PDF