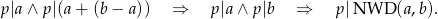Zadanie nr 1122197
Uzasadnij, że dla dowolnych liczb naturalnych 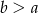 zachodzi równość
zachodzi równość 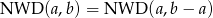 .
.
Rozwiązanie
Wystarczy pokazać, że liczba 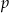 dzieli lewą stronę wtedy i tylko wtedy, gdy dzieli prawą stronę.
dzieli lewą stronę wtedy i tylko wtedy, gdy dzieli prawą stronę.
Jeżeli 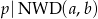 to
to 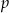 dzieli i
dzieli i  i
i 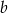 i mamy
i mamy

Na odwrót, jeżeli 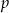 dzieli
dzieli  i
i 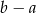 to mamy
to mamy