Zadanie nr 4821357
Liczby pierwsze 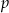 i
i 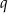 , gdzie
, gdzie 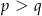 , nazywamy bliźniaczymi, jeżeli
, nazywamy bliźniaczymi, jeżeli 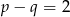 . Udowodnij, że liczby pierwsze
. Udowodnij, że liczby pierwsze 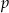 i
i 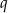 są bliźniacze wtedy i tylko wtedy, gdy
są bliźniacze wtedy i tylko wtedy, gdy 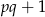 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Rozwiązanie
Załóżmy najpierw, liczby 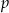 i
i 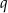 są bliźniacze. W takim razie
są bliźniacze. W takim razie
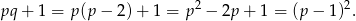
Teraz w drugą stronę. Mamy
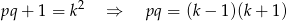
Prawa strona jest iloczynem dwóch liczb naturalnych większych od 1. Skoro 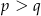 są liczbami pierwszymi, musi być
są liczbami pierwszymi, musi być
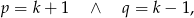
czyli 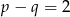 .
.

