/Konkursy/Zadania/Liczby/Całkowite/Podzielność

Zadanie nr 5153722

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że liczb pierwszych jest nieskończenie wiele.

Rozwiązanie

Załóżmy, że liczb pierwszych jest skończenie wiele i wypiszmy je wszystkie: 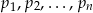p 1,p 2,...,pn . Zauważmy, że liczba

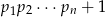
p1p2 ⋅⋅⋅pn + 1

nie dzieli się przez żadną z liczb 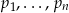p 1,...,pn (bo przy dzieleniu przez każdą z nich daje resztę 1), więc musi to być liczba pierwsza (bo nie ma żadnych dzielników pierwszych mniejszych od siebie). Jest ona większa od każdej z liczb 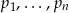p1,...,pn co stanowi sprzeczność z naszym założeniem.

Zauważmy, że na ogół z tego, że liczby 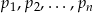p 1,p2,...,pn są pierwsze wcale nie wynika, że liczba

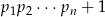
p p ⋅⋅⋅p + 1 1 2 n

jest pierwsza. Np.

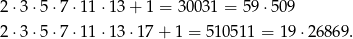
2⋅ 3⋅5 ⋅7 ⋅11⋅ 13+ 1 = 3003 1 = 59 ⋅509 2⋅ 3⋅5 ⋅7 ⋅11⋅ 13⋅ 17+ 1 = 5105 11 = 19 ⋅26869 .

Zawsze jednak liczba ta musi mieć dzielniki pierwsze większe od liczb 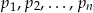p 1,p 2,...,pn i dlatego założenie, że liczb pierwszych jest skończenie wiele doprowadziło nas do sprzeczności.

Wersja PDF