/Konkursy/Zadania/Liczby/Całkowite/Podzielność

Zadanie nr 7597032

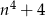Znajdź wszystkie liczby naturalne n takie, że liczba 4 n + 4 jest liczbą pierwszą.

Wersja PDF

Rozwiązanie

Rozkładamy podany wielomian na czynniki.

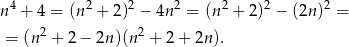
4 2 2 2 2 2 2 n + 4 = (n + 2) − 4n = (n + 2) − (2n) = = (n 2 + 2 − 2n )(n2 + 2+ 2n).

Jeżeli powyższy iloczyn ma być liczbą pierwszą, to jeden z czynników musi być równy 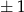± 1 (bo liczba pierwsza może mieć tylko jeden czynnik różny od 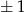± 1 ). Ponadto

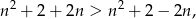
2 2 n + 2+ 2n > n + 2 − 2n ,

więc to 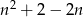2 n + 2− 2n musi być równe 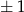± 1 . Ponieważ

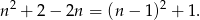
2 2 n + 2 − 2n = (n − 1) + 1.

musimy mieć 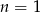n = 1 .  
Odpowiedź: n = 1

Wersja PDF