Zadanie nr 7828056
Wyznacz najmniejszą liczbę 4-cyfrową, która przy dzieleniu przez 7 daje resztę 6, a przy dzieleniu przez 6 daje resztę 5.
Rozwiązanie
Można taką liczbę znaleźć sprawdzając kolejne liczby czterocyfrowe, ale można też postąpić tak: wiemy, że szukana liczba ma mieć postać 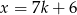 . W takim razie
. W takim razie
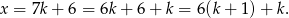
To oznacza, że reszta z dzielenia przez 6 liczby  jest taka sama jak reszta z dzielenia przez 6 liczby
jest taka sama jak reszta z dzielenia przez 6 liczby 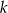 . Zatem
. Zatem 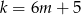 i
i
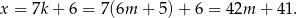
Teraz wystarczy tylko znaleźć najmniejszą liczbę 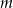 , dla której liczba
, dla której liczba  jest 4-cyfrowa. Takie
jest 4-cyfrowa. Takie 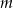 możemy wyznaczyć rozwiązując nierówność
możemy wyznaczyć rozwiązując nierówność 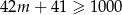 . Szukaną liczbę otrzymamy dla
. Szukaną liczbę otrzymamy dla 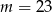 i jest to 1007.
i jest to 1007.
Odpowiedź: 1007

