Zadanie nr 8572907
Dla jakich liczb całkowitych  liczba
liczba 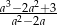 jest także liczbą całkowitą?
jest także liczbą całkowitą?
Rozwiązanie
Postępujemy tak jakby to był zwykły ułamek, najpierw robimy z niego ułamek właściwy, czyli dzielimy licznik przez mianownik z resztą. My to zrobimy grupując wyrazy.
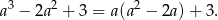
Tak więc podane wyrażenie jest równe
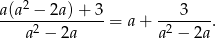
Liczba ta będzie całkowita tylko wtedy, gdy 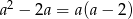 jest dzielnikiem 3, czyli jest równe -3,-1,1 lub 3. Można oczywiście rozwiązać 4 równania kwadratowe, ale prościej jest skorzystać z faktu, że
jest dzielnikiem 3, czyli jest równe -3,-1,1 lub 3. Można oczywiście rozwiązać 4 równania kwadratowe, ale prościej jest skorzystać z faktu, że  też jest całkowite. W szczególności liczba
też jest całkowite. W szczególności liczba 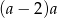 jest iloczynem dwóch liczb całkowitych odległych o 2, a więc na pewno nie jest równa 1 (bo ma przynajmniej jeden dzielnik różny od 1). Jeżeli
jest iloczynem dwóch liczb całkowitych odległych o 2, a więc na pewno nie jest równa 1 (bo ma przynajmniej jeden dzielnik różny od 1). Jeżeli 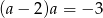 , to jedna liczba musiałaby być dodatnia a jedna ujemna i ponieważ są odległe o 2, to nie da się ich tak dobrać.
, to jedna liczba musiałaby być dodatnia a jedna ujemna i ponieważ są odległe o 2, to nie da się ich tak dobrać.
Jeżeli 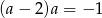 to
to 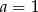 .
.
Pozostaje przypadek 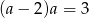 . Mamy wtedy dwa rozwiązania
. Mamy wtedy dwa rozwiązania 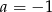 i
i 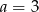 .
.
Odpowiedź: